Hány olyan háromszög van, melynek oldalai egész hosszúságúak, és a leghosszabb oldala 11 egység hosszú? (Csak a nem elfajuló háromszögeket számoljuk, melyeknek nincs  $ 0^{\circ}$  -os szöge.)
Ha a kapott szám  $n$  , a válasz  $n$  és  $ 14$  legkisebb közös többszöröse.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Halhatatlan kapitánynak három halhatatlan unokája van, akiknek életkora három különböző prímszám és ezek négyzetének összege is prímszám. Hány éves a kapitány legkisebb unokája? (Ne feledjük, hogy az unokák halhatatlanok, így életkoruk nagyon nagy szám is lehet!)
Ha a kapott szám  $n$  , a válasz  $ 2018-14\cdot n$  értéke.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen  $f(x) = \left|1-2x\right|$  a  $\left[0,1 \right]$  intervallumon értelmezett függvény. Hány megoldása van az  $f(f(f(x)))=\dfrac{x}{2}$  egyenletnek?
A válasz a megoldások számának tizennégyszerese.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A  $P$  pont az  $ABCD$  négyzet síkjának egy olyan pontja, melyre teljesül, hogy a \linebreak  $PAB, PBC, PCD, PDA$  háromszögek mindegyike egyenlő szárú háromszög. Hány ilyen  $P$  pont van? (Nem számoljuk az elfajuló háromszögeket, melyeknek van  $ 0^{\circ}$  -os szöge.)
\emph{Ha a kapott szám  $n$  , a válasz  $\dfrac{n}{14}$  törtrésze tízezerszeresének egészrésze.}

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Tekintsük a  $ 2x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} +x_{8} + x_{9} + x_{10} = 3$  egyenletet. Hány nemnegatív egészekből álló megoldása van? Ha a kapott szám  $n$  , a válasz  $n+14$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ábrán látható áramköri részletben minden kapcsoló egymástól függetlenül  $\dfrac{1}{2}$  -  $\dfrac{1}{2}$  valószínűséggel van nyitva vagy zárva. Mi a valószínűsége annak, hogy  $A$  -tól  $B$-ig eljut az áram?

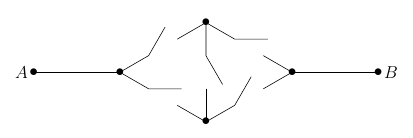
A válasz az eredményül kapott racionális szám tovább nem egyszerűsíthető alakjában a számlálónak, a nevezőnek és 2018-nak az összege.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Határozzuk meg azt a két legkisebb pozitív egészet, amelynek 13-szorosát 7-es számrendszerben felírva az utolsó előtti számjegy 4, az utolsó számjegy pedig 3.
A válasz a két szám növekvő sorrendben, egymás után írva.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen  $ABCD$  tetszőleges négyszög, és legyenek  $A_{1}, B_{1}, C_{1}, D_{1}$  rendre a  $BCD,ACD, ABD,$  illetve  $ABC$  háromszögek súlypontjai. Határozzuk meg az  $A_{1}, B_{1}, C_{1}, D_{1}$  négyszög és az  $ABCD$  négyszög területének arányát.
A válasz a kapott racionális szám tovább nem egyszerűsíthető alakjában a nevező tizennégyszeresének és a számlálónak az összege.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen bármely két  $x$  és  $y$  valós számra  $x \sim y = ax +by +cxy$  , ahol  $a, b, c$  konstansok. Tudjuk, hogy  $ 1\sim2 = 3$  és  $ 2 \sim 3 = 4$  és létezik egy olyan  $d$  nem nulla, valós szám, hogy  $x\sim d = x$  minden valós  $x$  esetén teljesül.
A válasz  $d\sim (-2018)$  értéke.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Tizenhat város mindegyike nevezett egy  $A$  és egy  $B$  csapatot egy focibajnokságba. A bajnokság során egy tetszőleges csapatnak a saját városa másik csapata kivételével mindegyik csapattal meg kell küzdenie. Valamikor a verseny során az egyik város  $A$  csapata észrevette, hogy mindegyik másik csapat különböző számú mérkőzést játszott. Hány mérkőzést játszott ennek a városnak a  $B$  csapata?
Ha a kapott szám  $n$  , akkor a válasz  $n+14$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az  $ABC$  háromszög  $A$  -nál,  $B$  -nél,  $C$  -nél levő szögeit jelölje rendre  $\alpha, \beta, \gamma$  . Ha  $\sin \alpha= 3/5$  és  $\cos \beta = 5/13$  , akkor mennyi  $\cos \gamma$  értéke?
A válasz a kapott tört legegyszerűbb alakjában a számláló majd a nevező egymás után írva.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az  $ 1, 4, 8, 10, 16, 8, 21, 25, 30, 43$  számsorozatnak hány olyan egymást követő tagokból álló részsorozata van, amelyben a tagok összege osztható  $ 11$  -gyel?
A válasz  $ 2018-n$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Hány különböző megoldása van a  $\cos \dfrac{x}{4} = \cos x$  egyenletnek a  $(0;24\pi)$  intervallumon?
Ha az eredmény  $n$  , a válasz  $n + 14^{2}$

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy szabályos oktaéder minden éle  $ 3$  egység hosszú. Mindegyik csúcsánál vágjunk le egy-egy szabályos, egység oldalú négyzet alapú gúlát. A kapott poliédernek  $k$  éle van, ezeket megszámozzuk az 1, 2, ...,  $k$  számokkal. Határozd meg, hány olyan  $(i;j)$  számpár van  $(1 \leq i< j \leq k)$  , hogy a poliéder  $i.$  és  $j.$  élei kitérő egyenesek.
Ha a kapott szám  $n$  , akkor a válasz  $n+1144$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy ország a szigetvilágban  $N$  szigetet tartalmaz, legyenek ezek  $A_1, A_2, \ldots, A_N$  . A Közlekedési Hatóság hidak építését tervezi, hogy autóval el lehessen jutni bármely szigetről bármely másikra néhány hídon át. Technikai okok miatt hidat csak  $A_i$  -ből  $A_{i+1}$  -be lehet építeni  $(i = 1,2 \ldots, N-1)$  vagy  $A_i$  -ből  $A_N$  -be, ha  $i < N$  . A hidak építésére terveket készítenek. Nevezzünk egy tervet jónak, ha az eddigi követelmények teljesülnek, de bármely hidat kihagyva már nem. Legyen a jó tervek száma  $a_N$  . Például  $a_1=1$  (az egyetlen jó terv, ha nincs is híd), és  $a_2=1$  (van egy híd a két sziget között).
A válasz  $a_6+14$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy sorban  $ 8$  ember ül, összesen  $ 4$  országból érkeztek, mindegyik országból pontosan ketten. Hány olyan permutációja létezik a  $ 8$  embernek, melyre teljesül, hogy bármely két szomszédos ember különböző országból érkezett?
Ha a kapott szám  $n$  , akkor a válasz  $n-10000$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen  $A=\{1,2,3,4,5\}$  és  $B=\{1,2,3\}$  . Az  $f$  egy jó függvény, ha az értelmezési tartománya  $A$  , értékkészlete pedig részhalmaza  $A$  -nak. Hány olyan jó  $f$  függvény van, amire teljesül az is, hogy az  $f(f(x))$  értékkészlete pont a  $B$  halmaz?
Ha a kapott szám  $n$  , akkor a végeredmény  $n+1414$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Hányféleképpen lehet egy  $ 3 \times 10$  -es téglalapot  $ 2 \times 1$  -es dominókkal kirakni?
A válasz a kapott szám  $ 14$  -szerese.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy hexa-bitetraéder és egy szabályos oktaéder lapjai egybevágó szabályos háromszögek. A két poliéder beírt gömbje sugarának hányadosa legyen  $m/n$  , ahol  $(m,n)=1$  . (A hexa-bitetraéder hat darab szabályos háromszöglappal rendelkezik, mintha két tetraédert egy lapjuk mentén összeragasztanánk.)
A válasz  $ 14mn +14m +n$  értéke.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A válasz  $ 2018+n$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba