Egy fafajta törzsének keresztmetszetét vizsgáljuk egy adott magasságban. Ez a kereszt- metszet a fa 5 és 20 éves kora közötti növekedése során (jó közelítéssel) mindvégig kör alakúnak tekinthető. A kör átmérőjét a $d: [5; 20] \rightarrow \mathbb{R}, d(x) = -0, 25x^2 + 20 x + 40$ függvény adja meg, ahol $x$ a fa években mért életkorát, $d(x)$ pedig az átmérő milliméterben mért hosszát jelöli.

a) Hány cm a törzs keresztmetszetének átmérője akkor, amikor a fa éppen 10 éves?

b) Hány $dm^2$-rel nő a fatörzs keresztmetszetének területe a 11. évben? Válaszát egy tizedesjegyre kerekítve adja meg!

c) Hány éves a fa akkor, amikor a törzs keresztmetszetének kerülete éppen 1 méter?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Oldja meg az alábbi két egyenlőtlenséget a valós számok halmazán!

a) $\cos x\ge \dfrac{1}{2}$

b) $\sqrt{\dfrac{x}{5}-4}<20$

c) Hány olyan egész szám van, amelyik gyöke az alábbi egyenlőtlenségnek? $ \log_{0,5} (2 x + 100) \ge -8$

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A $p, q, r$ pozitív számok összege 180. Tudjuk továbbá, hogy $p : q = 7 : 8$ és $r : p = 5 : 3$.

a) Határozza meg ezeket a számokat!

A H halmaz az első 90 pozitív egész szám halmaza. H-ból véletlenszerűen kiválasztunk két különböző számot.

b) Határozza meg annak a valószínűségét, hogy a két kiválasztott szám egy derékszögű háromszög (fokban mért) valamelyik két szöge!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

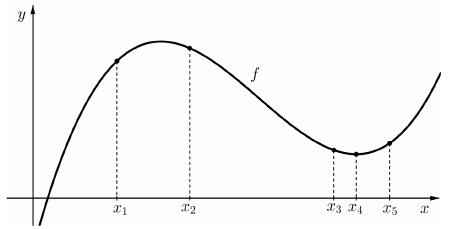
a) Az ábrán a harmadfokú $f$ függvény grafikonjának egy részlete látható. A függvény értelmezési tartományában megjelöltünk öt helyet. Mindegyik esetben döntse el, hogy az adott helyen az f első, illetve második deriváltjának előjele pozitív (P) vagy negatív (N)! Válaszát írja a megadott táblázat meg- felelő cellájába! (Tudjuk, hogy $f'( x_4 ) = 0$ .)

b) Adott az $y = - \dfrac{1}{4}( x --2)^2 + 8$ egyenletű parabola. Határozza meg a $k$ valós paraméter értékét úgy, hogy a $ 4x – y = k$ egyenletű egyenes érintse a parabolát, és határozza meg az érintési pont koordinátáit is!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba