Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
10 707 685 Mai:
3 203 18-97-9-174.crawl.commoncrawl.org
(IP: 18.97.9.174) HonlapokSULINET Matematika Oktatási Hivatal Versenyvizsga portál Matematika Portálok |
1. találat: Matematika középszintű érettségi, 2013. május, I. rész, 1. feladat Témakör: *Halmazok ( unió, különbség) (Azonosító: mmk_201305_1r01f ) Az A és B halmazokról tudjuk, hogy $A \cup B = \{1;2;3;4;5;6;7;8;9 \}$ és $B \setminus A =\{1;2;4;7\}$. Elemeinek felsorolásával adja meg az A halmazt! Témakör: *Statisztika ( átlag) (Azonosító: mmk_201305_1r02f ) Egy kis cégnél nyolcan dolgoznak: hat beosztott és két főnök. A főnökök átlagos havi jövedelme 190 000 Ft, a beosztottaké 150 000 Ft. Hány forint a cég nyolc dolgozójának átlagos havi jövedelme? 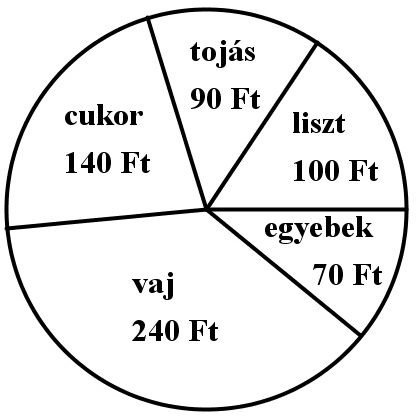Témakör: *Geometria ( arány, algebra) (Azonosító: mmk_201305_1r03f ) Az ábra egy sütemény alapanyagköltségeinek megoszlását mutatja. Számítsa ki a „vaj” feliratú körcikk középponti szögének nagyságát fokban! Válaszát indokolja!
Témakör: *Függvények ( abszolútérték) (Azonosító: mmk_201305_1r04f ) Az alábbi hozzárendelési utasítással megadott, a valós számok halmazán értelmezett függvények közül kettőnek egy-egy részletét ábrázoltuk. Adja meg a grafikonokhoz tartozó hozzárendelési utasítások betűjelét!
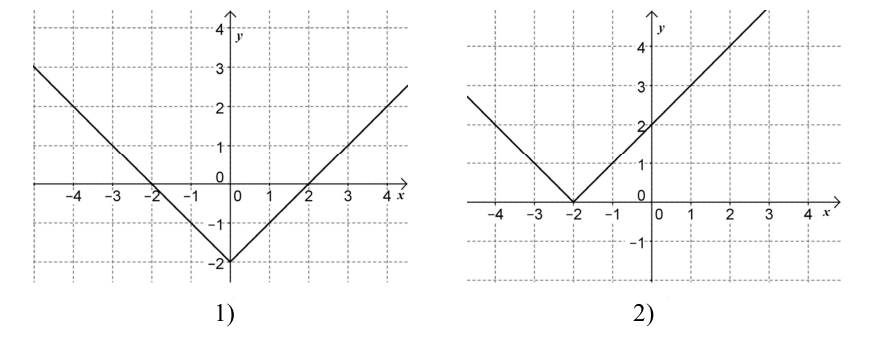
$A) \ x\mapsto |x+2| \qquad B) \ x\mapsto |x-2| \qquad C) \ x\mapsto |x|-2 \qquad D) \ x\mapsto |x|+2$ Témakör: *Geometria ( trigonometria, szögfüggvény) (Azonosító: mmk_201305_1r05f ) A vízszintessel 6,5°-ot bezáró egyenes út végpontja 124 méterrel magasabban van, mint a kiindulópontja. Hány méter hosszú az út? Válaszát indokolja! Témakör: *Koordinátageometria (Azonosító: mmk_201305_1r06f ) Adja meg a 2x + y = 4 egyenletű egyenes és az x tengely M metszéspontjának a koordinátáit, valamint az egyenes meredekségét! Témakör: *Függvények ( parabola) (Azonosító: mmk_201305_1r07f ) Adja meg az $x\mapsto x^2+10x+21 \quad (x \in \mathbb{R})$ másodfokú függvény minimumhelyét és minimumának értékét! Válaszát indokolja! Témakör: *Logika ( statisztika, geometria, algebra) (Azonosító: mmk_201305_1r08f ) Adja meg a következő állítások logikai értékét (igaz vagy hamis)! A) A {0; 1; 2; 3; 4} adathalmaz szórása 4. B) Ha egy sokszög minden oldala egyenlő hosszú, akkor a sokszög szabályos. C) A 4 és a 9 mértani közepe 6. Témakör: *Térgeometria ( hasonlóság, arány) (Azonosító: mmk_201305_1r09f ) Két gömb sugarának aránya 2 : 1. A nagyobb gömb térfogata k-szorosa a kisebb gömb térfogatának. Adja meg k értékét! Témakör: *Kombinatorika ( permutáció) (Azonosító: mmk_201305_1r10f ) Egy futóverseny döntőjébe hat versenyző jutott, jelöljük őket A, B, C, D, E és F betűvel. A cél előtt pár méterrel már látható, hogy C biztosan utolsó lesz, továbbá az is biztos, hogy B és D osztozik majd az első két helyen. Hányféleképpen alakulhat a hat versenyző sorrendje a célban, ha nincs holtverseny? Válaszát indokolja! Témakör: *Statisztika (Azonosító: mmk_201305_1r11f ) Réka év végi bizonyítványában a következő osztályzatok szerepelnek: 4; 2; 3; 5; 5; 4; 5; 5; 4. Adja meg Réka osztályzatainak móduszát és mediánját! Témakör: *Valószínűségszámítás ( számelmélet) (Azonosító: mmk_201305_1r12f ) Adja meg annak valószínűségét, hogy a 7, 8, 9, 10, 11, 12, 13, 14 számok közül egyet véletlenszerűen kiválasztva a kiválasztott szám prím!
|
KeresésHonlapokKözépiskolai Matematikai és Fizikai Lapok Wolfram Alpha Art of Problem Solving Kvant IMO |
|||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
| |||||||||||||||||||
| |||||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
|
1082 Budapest, Horváth Mihály tér 8. OM azonosító: 035277 |
Joomla template: szsnjm4-001 (c) Szoldatics József 2011/2025
www.szolda.hu
www.szolda.hu