Renáta feljegyezte egy tizenhat élű, hétpontú egyszerű gráf minden pontjának fokszámát, és megállapította, hogy a fokszámok között csak kétféle érték szerepel. Mi lehet ebben a gráfban a pontok fokszáma?

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Hány olyan $ k $ pozitív egész szám van, amelyre az $A =\dfrac{1!\cdot 2!\cdot 3!\cdot \ldots \cdot 10!}{k}$ kifejezés értéke négyzetszám?

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Határozza meg azokat a $ p $ és $ q $ pozitív prímszámokat, amelyekre

$ \log_2(q-1) + \log_4 (q + 1) = 1 + 3\log_8 p $

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

A Nekeresd Iskola $ n $ fős tizenegyedik évfolyamából
- a szalagavató bál szervezésére a $ k $ tagú $ S $,
- a gólyatábor szervezésére a $ k + 1 $ tagú $ G $,
- a ballagás szervezésére a $ k + 2 $ tagú $ B $
csoportot kell kiválasztani úgy, hogy az évfolyam minden tanulója akár több csoport tagja is lehet ($ 3 \le k + 2 \le n $). A $ G $ csoportot 4-szer annyiféleképpen lehet kialakítani, mint az $ S $ csoportot, míg a $ B $ csoportot $\dfrac{38}{3}$-szor annyiféleképpen lehet kialakítani, mint az $ S $ csoportot. Hányféleképpen választható ki 3 tanuló az $ n $ fős évfolyamból?

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

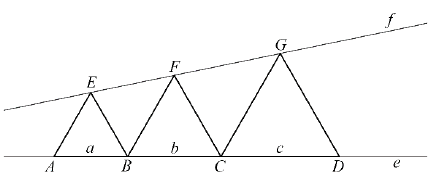
Adott a síkon az $ e $ és az $ f $ egyenes, valamint az ábrának megfelelően az $ ABE $, $ BCF $, $ CDG $ szabályos háromszög ($ A, B, C, D \in e$ és $E, F, G \in f$ ), ahol a háromszögek oldalai rendre $ a $, $ b $ és $ c $ ($ a < b < c$).

a)  Igazolja, hogy $ b^2 = ac $.

b)  Igazolja, hogy az a, b és c oldalakból pontosan akkor szerkeszthető háromszög, ha

$ 1<\dfrac{c}{a}<\dfrac{3+\sqrt{5}}{2}$

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba