|
Menü
|
Adott
az  szög, valamint egy pozitív a szám. Keressük
meg a szögtartományban azokat a P
pontokat, amelyeknek a szögszáraktól mért távolságösszege az
adott a
számmal egyenlő! szög, valamint egy pozitív a szám. Keressük
meg a szögtartományban azokat a P
pontokat, amelyeknek a szögszáraktól mért távolságösszege az
adott a
számmal egyenlő! |
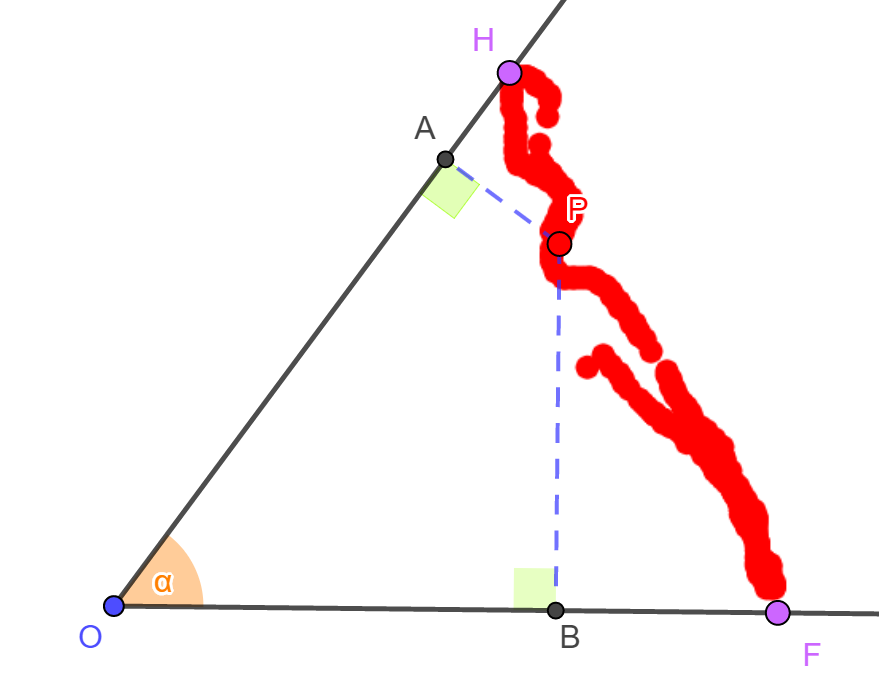
Az animációban a P pont szögszárakra
eső merőleges vetületét A
és B
jelöli. Segítségül a feltételeknek megfelelő, az adott szög száraira illeszkedő
pontokat (H
és F) a
szerkesztésben megadtuk. Ha megfelelően mozgatjuk a P pontot, akkor az
alábbi ábrához hasonló képet kapunk, amely olyan sejtés
megfogalmazására bíztat minket, hogy a megfelelő P pontok a HF szakaszra
illeszkednek.
Sejtésünk
igazolásához tegyük fel, hogy a P pontra teljesül hogy 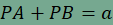 , majd toljuk el a szög g szárát a g-re merőleges, a hosszúságú vektorral! A kapott szögszárat g', az A pont képét A', f és g' metszéspontját F jelöli. Ekkor , majd toljuk el a szög g szárát a g-re merőleges, a hosszúságú vektorral! A kapott szögszárat g', az A pont képét A', f és g' metszéspontját F jelöli. Ekkor 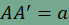 , ,
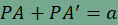 ,
amit ha összevetünk a
feltétellel, akkor azt kapjuk, hogy 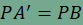 . Ez azt jelenti, hogy P illeszkedik az f és g' szögszárak által határolt megfelelő szögtartomány szögfelezőjére (az ábrán az . Ez azt jelenti, hogy P illeszkedik az f és g' szögszárak által határolt megfelelő szögtartomány szögfelezőjére (az ábrán az 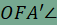 ). Ha a szögfelező a g szögszárat H-ban metszi, akkor tekintettel arra, hogy P az szögtartomány pontja, P a HF szakaszra illeszkedik. ). Ha a szögfelező a g szögszárat H-ban metszi, akkor tekintettel arra, hogy P az szögtartomány pontja, P a HF szakaszra illeszkedik.
Állításunk megfordítása is igaz. Ha a HF szakasz egy P pontját tekintjük, akkor annak távolsága a g' és f szögszáraktól egyenlő, és így az 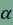 szög száraitól mért távolságösszege éppen az adott a állandó. szög száraitól mért távolságösszege éppen az adott a állandó.
Összefoglalva: a keresett P pontok az f és g' szárak által határolt szög szögfelezőjének 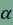 szögtartományba eső szakaszát alkotják. szögtartományba eső szakaszát alkotják.
|
|
 szög, valamint egy pozitív a szám. Keressük
meg a szögtartományban azokat a P
pontokat, amelyeknek a szögszáraktól mért távolságösszege az
adott a
számmal egyenlő!
szög, valamint egy pozitív a szám. Keressük
meg a szögtartományban azokat a P
pontokat, amelyeknek a szögszáraktól mért távolságösszege az
adott a
számmal egyenlő!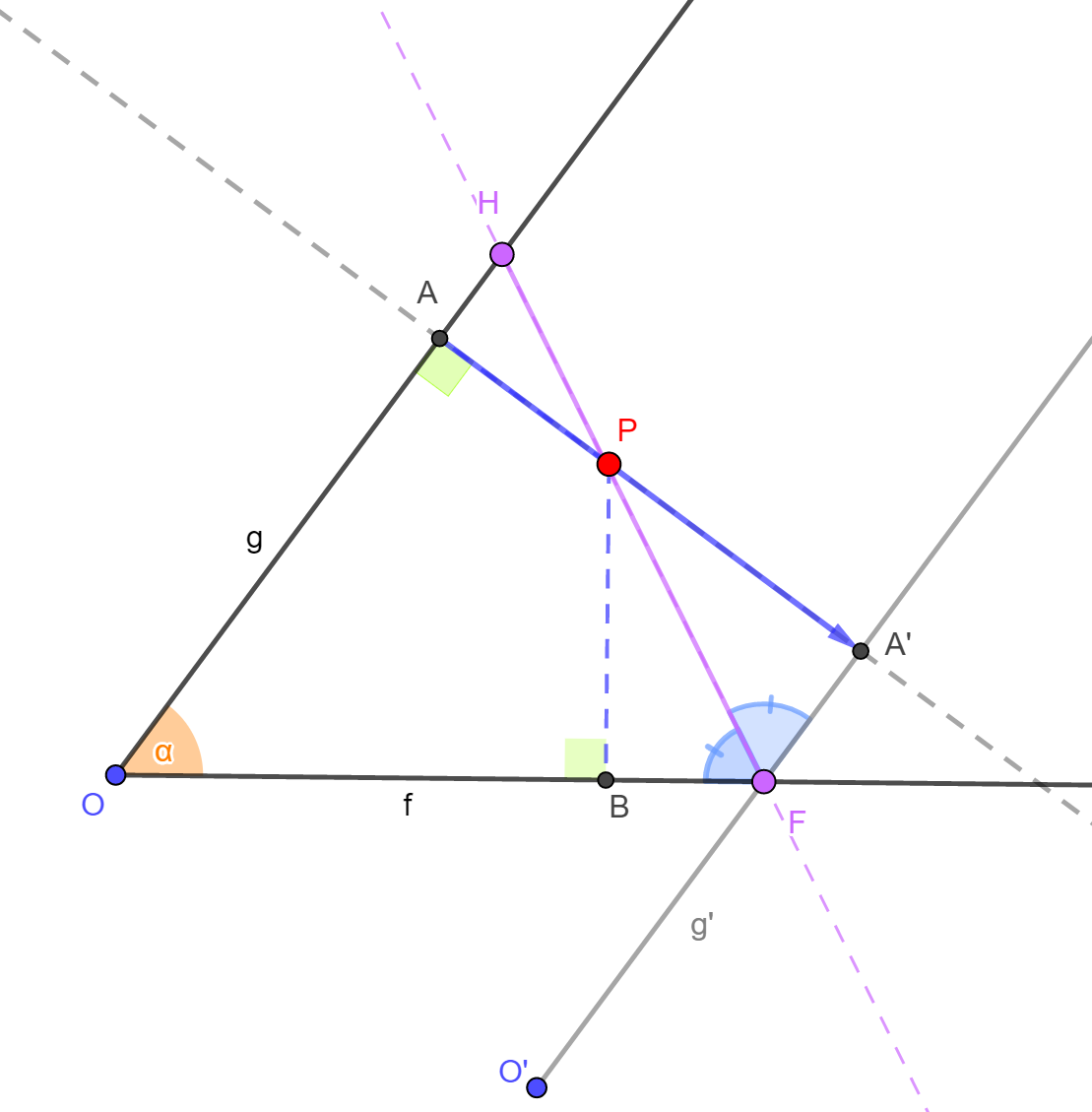
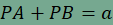 , majd toljuk el a szög
, majd toljuk el a szög 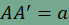 ,
,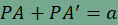 ,
,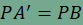 . Ez azt jelenti, hogy
. Ez azt jelenti, hogy 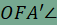 ). Ha a szögfelező a
). Ha a szögfelező a 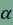 szög száraitól mért távolságösszege éppen az adott
szög száraitól mért távolságösszege éppen az adott