|
Menü
|
Az ABCD négyszög AB illetve CD oldalának felezőpontja E illetve F. Vizsgáljuk meg, hogy melyek azok a négyszögek, amelyekben  teljesül! Milyen kapcsolat van az AD és BC oldalak hosszának összege, valamint az EF középvonal hossza között? teljesül! Milyen kapcsolat van az AD és BC oldalak hosszának összege, valamint az EF középvonal hossza között? |
A
négyszögekkel kapcsolatos ismereteink alapján tudjuk, hogy a trapéz
középvonala párhuzamos az alapokkal, és hossza az alapok számtani
közepe, ezért ha ABCD trapéz, amelynek alapjai AD és BC, akkor 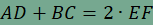 .
Az animáció segítségével meggyőződhetünk arról, hogy nincs olyan
további négyszög, amelyre az egyenlőség teljesül. Pontosabban: minden
négyszögben .
Az animáció segítségével meggyőződhetünk arról, hogy nincs olyan
további négyszög, amelyre az egyenlőség teljesül. Pontosabban: minden
négyszögben 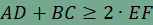 , ,
továbbá egyenlőség pontosan akkor teljesül, ha ABCD trapéz, melynek alapjai AD és BC. Ennek igazolásához toljuk el az AD oldalt az 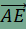 vektorral, a BC oldalt pedig a vektorral, a BC oldalt pedig a 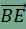 vektorral. A kapott képpontokat D' és C' jelöli. Az eltolás tulajdonságai alapján ED'=AD és EC'=BC, továbbá DD' és CC' párhuzamosak az AB oldallal, hosszuk pedig megegyezik, épp az AB oldal fele. Ekkor azonban DD'CC' paralelogramma, amelynek CD és C'D' átlói felezik egymást. Ebből következik, hogy a C'D' szakasznak pont az F pont a felzőpontja. vektorral. A kapott képpontokat D' és C' jelöli. Az eltolás tulajdonságai alapján ED'=AD és EC'=BC, továbbá DD' és CC' párhuzamosak az AB oldallal, hosszuk pedig megegyezik, épp az AB oldal fele. Ekkor azonban DD'CC' paralelogramma, amelynek CD és C'D' átlói felezik egymást. Ebből következik, hogy a C'D' szakasznak pont az F pont a felzőpontja. Toljuk el végül az EC' szakaszt az 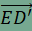 vektorral, a C' pont képét jelölje C''. Ekkor paralelogramma az EC'C''D' négyszög is, így D'C"=EC', továbbá EC'' átlójának felezőpontja megegyezik a C'D' szakasz felezőpontjával, vagyis F-fel. Ebből már következik, hogy E, F és C'' egy egyenesre illeszkednek, továbbá vektorral, a C' pont képét jelölje C''. Ekkor paralelogramma az EC'C''D' négyszög is, így D'C"=EC', továbbá EC'' átlójának felezőpontja megegyezik a C'D' szakasz felezőpontjával, vagyis F-fel. Ebből már következik, hogy E, F és C'' egy egyenesre illeszkednek, továbbá 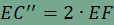 . Végül alkalmazzuk a háromszög-egyenlőtlenséget az EC''D' (esetleg elfajuló) háromszögben, így . Végül alkalmazzuk a háromszög-egyenlőtlenséget az EC''D' (esetleg elfajuló) háromszögben, így 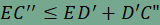 , ,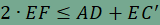 , ,
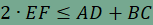 , ,
és pontosan ezt szerettük volna igazolni. Egyenlőség pontosan akkor teljesül, amikor az EC''D' háromszög elfajuló háromszög, azaz amikor E, D' és C'' egy egyenesre illeszkednek. Ennek feltétele, hogy ED' és D'C" párhuzamos legyen egymással, ami (szem előtt tartva a korábban megtalált paralelogrammákat) pontosan akkor teljesül, ha AD és BC is párhuzamosak, azaz ha az ABCD négyszög trapéz.
|
|
 teljesül! Milyen kapcsolat van az AD és BC oldalak hosszának összege, valamint az EF középvonal hossza között?
teljesül! Milyen kapcsolat van az AD és BC oldalak hosszának összege, valamint az EF középvonal hossza között?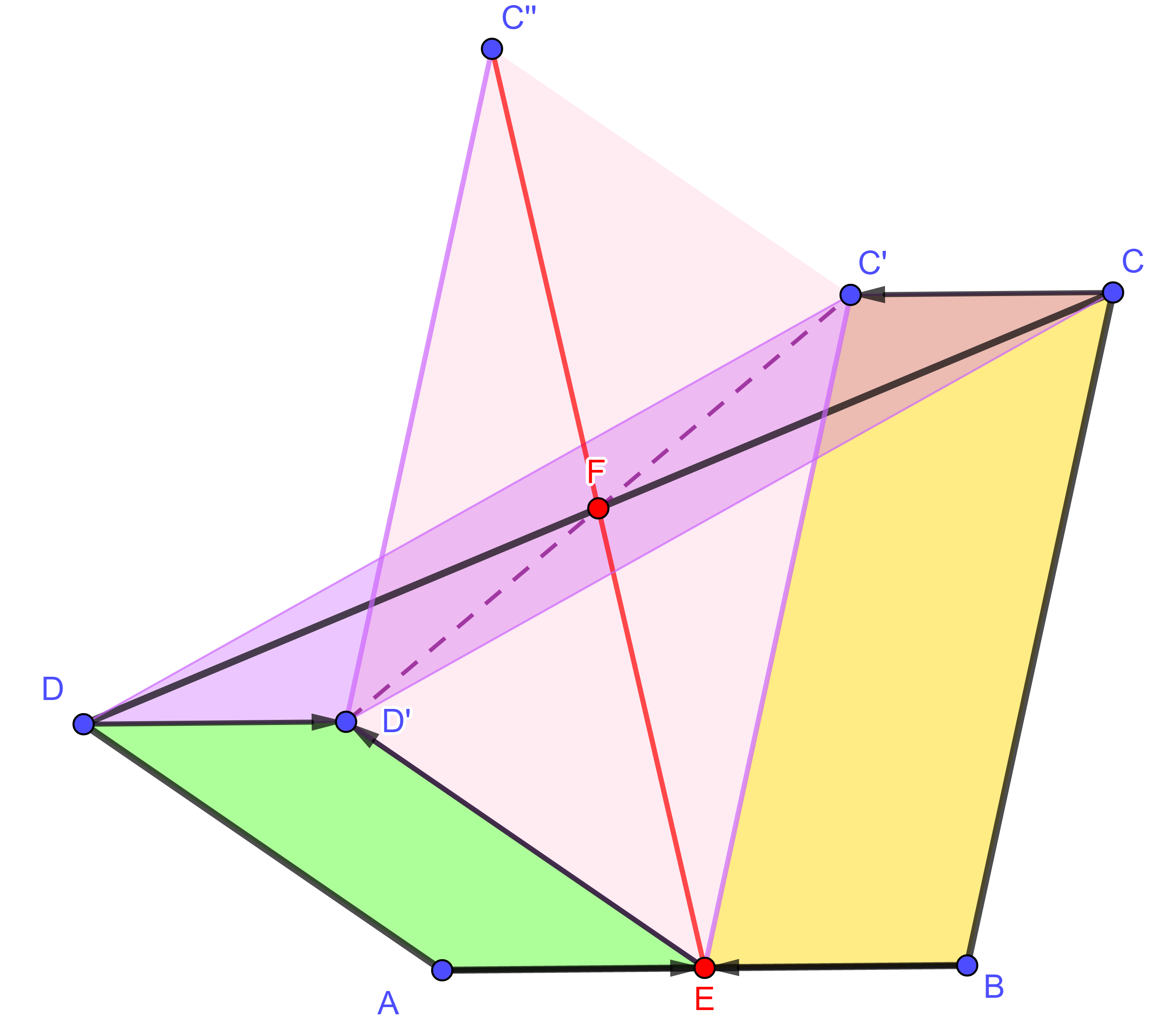
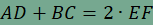 .
Az animáció segítségével meggyőződhetünk arról, hogy nincs olyan
további négyszög, amelyre az egyenlőség teljesül. Pontosabban: minden
négyszögben
.
Az animáció segítségével meggyőződhetünk arról, hogy nincs olyan
további négyszög, amelyre az egyenlőség teljesül. Pontosabban: minden
négyszögben 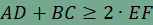
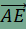 vektorral, a BC oldalt pedig a
vektorral, a BC oldalt pedig a 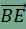 vektorral. A kapott képpontokat
vektorral. A kapott képpontokat 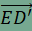 vektorral, a
vektorral, a 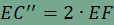 . Végül alkalmazzuk a háromszög-egyenlőtlenséget az
. Végül alkalmazzuk a háromszög-egyenlőtlenséget az 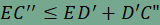 ,
,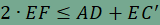 ,
,