|
Menü
|
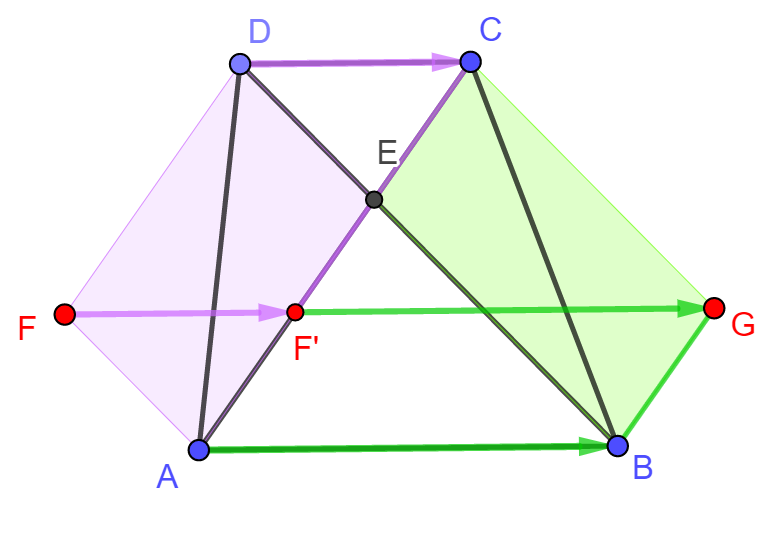
| Az ABCD trapéz alapjai AB és CD, átlóinak metszéspontja E. Az F és G pontokat úgy vesszük fel, hogy az AEDF és a BECG négyszögek paralelogrammák legyenek. Vizsgáljuk meg az FG szakaszt; mit állíthatunk helyzetéről és hosszáról? Indokoljuk válaszainkat! |
Az animáció segítségével megfogalmazható sejtések: az FG szakasz minden esetben párhuzamos az ABCD trapéz alapjaival, hossza pedig éppen az alapok hosszának összegével egyenlő.Sejtéseink igazolása előtt egy hasznos észrevételt teszünk: az AEDF paralelogrammában FD=AE, a BECG paralelogrammában pedig BG=EC, így 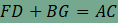 . Nyilvánvaló továbbá, hogy FD és BG párhuzamos egymással, hiszen mindkettő párhuzamos az AC átlóval. . Nyilvánvaló továbbá, hogy FD és BG párhuzamos egymással, hiszen mindkettő párhuzamos az AC átlóval.Ezután toljuk el az FD szakaszt a 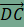 vektorral, és jelöljük az F
pont képét F'-vel. Az eltolás miatt FF'CD paralelogramma, így F'C
párhuzamos FD-vel, ezért F' illeszkedik az ABCD trapéz AC átlójára.
Mivel F'C=FD, ezért vektorral, és jelöljük az F
pont képét F'-vel. Az eltolás miatt FF'CD paralelogramma, így F'C
párhuzamos FD-vel, ezért F' illeszkedik az ABCD trapéz AC átlójára.
Mivel F'C=FD, ezért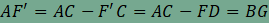 . Most toljuk el az AF' szakaszt az 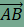 vektorral. Mivel AF' és BG egyenlők és párhuzamosak, ezért ABGF' paralelogramma, és így az eltolás az F' pontot a G pontba viszi át. Mindkét eltolás a trapéz alapjaival párhuzamos vektor mentén történt, amiből következik, hogy F, F' és G egy egyenesre illeszkednek, ráadásul az párhuzamos a trapéz alapjaival. Ebből már következik, hogy FG valóban párhuzamos a trapéz alapjaival. Mivel FF'=DC és F'G=AB, ezért vektorral. Mivel AF' és BG egyenlők és párhuzamosak, ezért ABGF' paralelogramma, és így az eltolás az F' pontot a G pontba viszi át. Mindkét eltolás a trapéz alapjaival párhuzamos vektor mentén történt, amiből következik, hogy F, F' és G egy egyenesre illeszkednek, ráadásul az párhuzamos a trapéz alapjaival. Ebből már következik, hogy FG valóban párhuzamos a trapéz alapjaival. Mivel FF'=DC és F'G=AB, ezért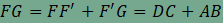 , azaz az FG szakasz hossza valóban az alapok hosszának összege.
|
|
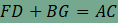 . Nyilvánvaló továbbá, hogy
. Nyilvánvaló továbbá, hogy 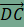 vektorral, és jelöljük az
vektorral, és jelöljük az 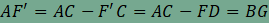 .
.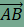 vektorral. Mivel
vektorral. Mivel 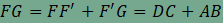 ,
,