| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
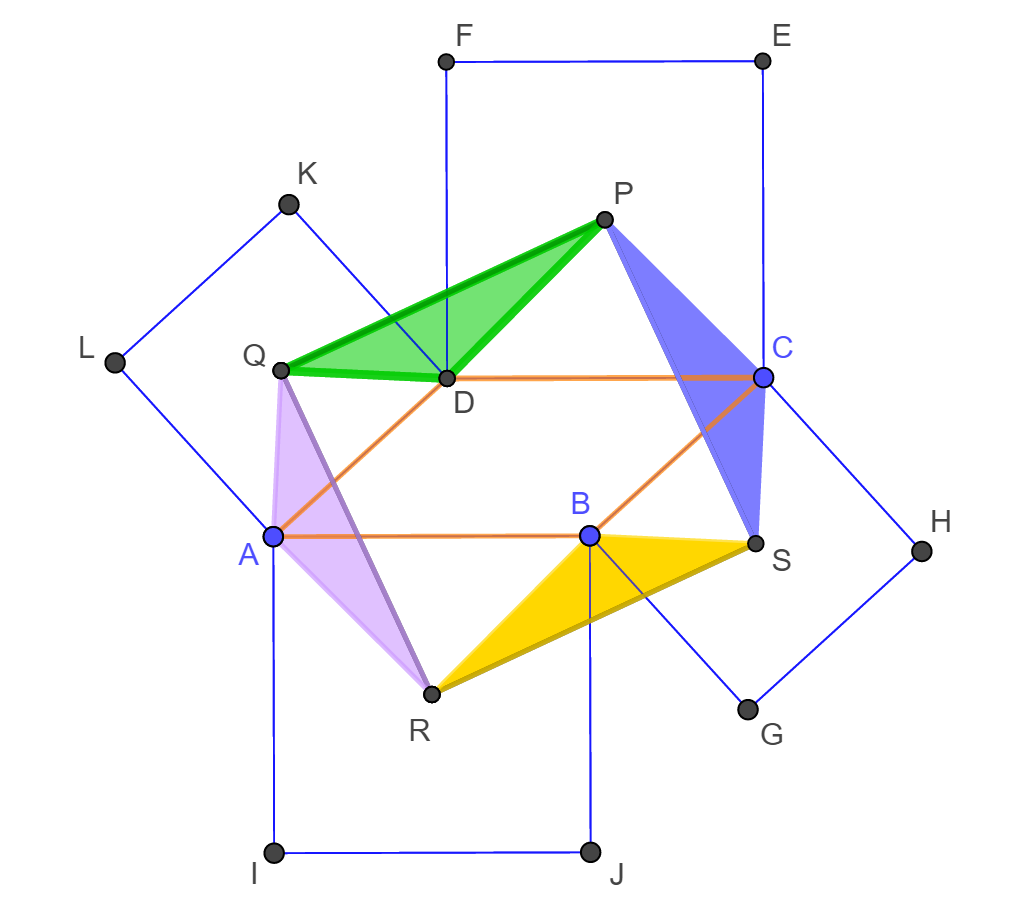
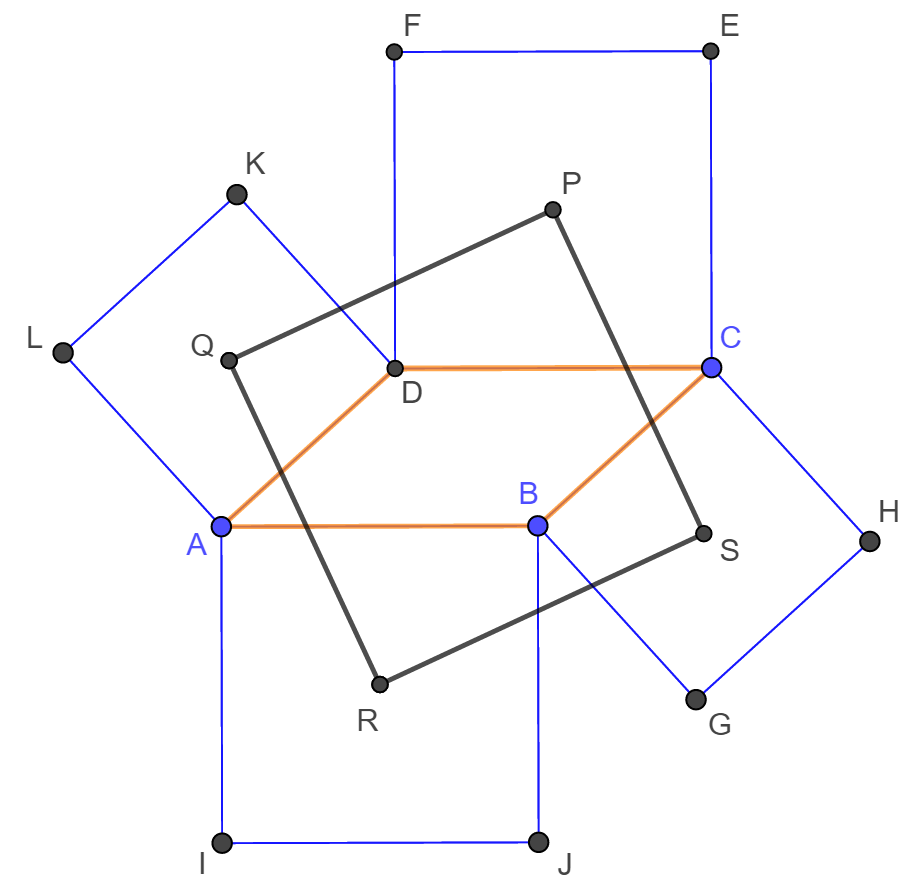
| Az ABCD paralelogramma oldalaira kifelé az ábra szerint négyzeteket rajzolunk. A négyzetek középpontja P, Q, R és S. Milyen négyszög a PQRS négyszög? |
Az animáció alapján megfogalmazható sejtés alapján a PQRS négyszög minden esetben négyzet.
Ennek igazolásához megmutatjuk, hogy a DQP, AQR, BSR és CSP háromszögek egybevágók egymással. Ebből már következik, hogy a PQRS négyszög rombusz. Tekintsük
a DQP és AQR háromszögeket!
Ezekben DQ=AQ és DP=AR, hiszen
páronként ugyanakkora oldalú négyzetek átlóinak felével egyenlők.
Másrészt ha az ABCD
paralelogramma A
csúcsánál lévő szöget
és
Mivel azonban
ezért
ami mutatja, hogy az AQR és DQP háromszögek nemcsak két-két oldalukban, hanem az általuk bezárt szögükben is megegyeznek, így a két háromszög egymással egybevágó. Ebből következően persze harmadik oldaluk is megegyezik, azaz PQ=RQ. Vegyük még észre, hogy AQ és DQ merőlegesek egymásra (a négyzet egy-egy átlójára illeszkednek), továbbá a két háromszög azonos körüljárási iránnyal rendelkezik, ezért a DQP háromszög a Q pont körüli -90°-os forgatással vihető át az AQR háromszögbe, amiről az alábbi animációban meg is győződhetünk. Mivel szakasz és elforgatott képe egymással a forgatás szögét zárja be, ezért QP és RQ merőlegesek egymásra. Hasonló gondolatmenettel igazolható, hogy az ábra összes színes háromszöge egybevágó egymással, továbbá a PQRS négyszög minden szöge 90°-os. A fentiekből adódóan a PQRS négyszög valóban négyzet.
|
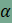 jelöli,
akkor
jelöli,
akkor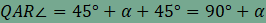 ,
,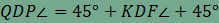 .
.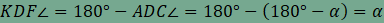 ,
,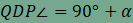 ,
,