| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
| Az
ABCD négyzet
AB,
CD,
BC
és DA
oldalán rendre felvesszük az E,
F,
G és
H
pontokat úgy, hogy EF
és GH
merőlegesek legyenek egymásra. Hogyan kell megválasztani a pontokat ha
azt akarjuk, hogy az AE+AH+CG+CF
összeg a lehető legkisebb,
illetve a lehető legnagyobb legyen? Mekkora az összeg minimuma és
maximuma? |
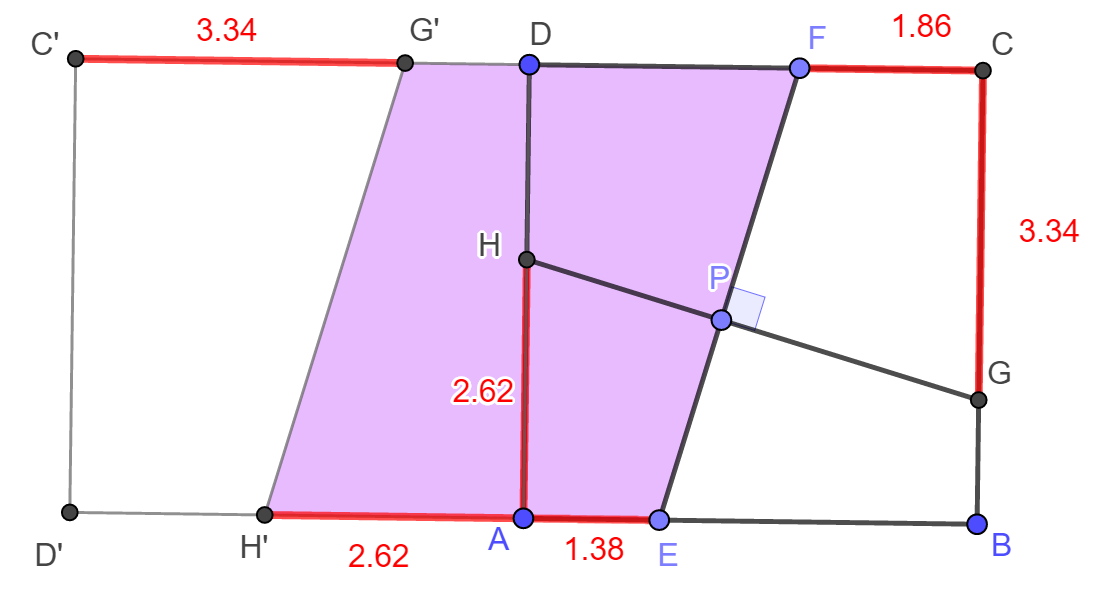
Az animáció alapján megfogalmazható sejtés alapján az AE+AH+CG+CF összeg mindig ugyanakkora. Ennek belátásához forgassuk el az ABCD négyzetet,valamint a HG szakaszt az A csúcs körül 90°-kal. A forgatás után az A csúcs helyben marad, a B csúcs képe D, a C csúcsé C', a D csúcsé D', míg a HG szakasz átmegy az ábrán H'G'-vel jelölt szakaszba. A forgatás ismert tulajdonsága, hogy szakasz és elforgatott képe a forgatás szögét zárja be egymással, ezért HG és H'G' merőlegesek egymásra. Mivel azonban EF is merőleges HG-re, ezért azonnal adódik, hogy H'G' és EF párhuzamosak, azaz a H'EFG' négyszög paralelogramma.
Vegyük figyelembe, hogy az AH szakasz elforgotott képe AH', és a CG szakaszé pedig C'G'. Ezek alapján ha az ABCD négyzet oldalát a jelöli, akkor a H'EFG' paralelogrammában EH'=FG', AH'+AE=G'D+DF, AH+AE=a-G'C'+a-CF, AH+AE=a-CG+a-CF. Az utóbbi egyenlőség átrendezés után az AH+AE+CG+CF=2a alakot ölti. Eredményünk mutatja, hogy a keresett összeg minden esetben az ABCD négyzet oldalának kétszerese, akárhol is helyezkednek az E, F, G és H pontok a négyzet oldalain. A minimum és a maximum is tehát 2a. Megjegyezzük, hogy állításunk megfordítható: ha az ABCD négyzet megfelelő oldalain úgy vesszük fel az E, F, G és H pontokat, hogy AH+AE+CG+CF=2a, ahol
a
az ABCD
négyzet oldalának hosszát jelöli, akkor EF és GH merőlegesek
egymásra.
A fenti állítás igazolásához ugyanúgy kell eljárnunk, mint az előbb. Ezúttal a 90°-os forgatás után előálló H'EFG' négyszögről a feltétel alapján belátható, hogy H'E=G'F, így a négyszög paralelogramma. Ekkor viszont H'G' párhuzamos EF-fel, és mivel H'G' merőleges a HG szakaszra (hisszen annak elforgatott képre), ezért EF is merőleges HG-re. |