Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
Vegyük
fel az ABC szabályos
háromszög AB, BC, valamint CA oldalán az F, D, valamint E pontokat úgy,
hogy ED és AB, valamint EF és CB párhuzamosak
legyenek.
Legyen továbbá az AD
szakasz D'
és a CF
szakasz F'
pontjára  . Mekkora
szöget zárnak be a CD'
és a BF'
egyenesek egymással? |
Mivel ED és AB párhuzamos egymással, ezért az ADC háromszög is szabályos, vagyis ED=DC. Az EF és a BC szakaszok párhuzamosságából adódik, hogy az FBDC négyszög paralelogramma, ezért ED=FB. A kapott egyenlőségek bal oldalán ugyanaz a kifejezés áll, ezért DC=FB. Ekkor viszont az ADC és CFB háromszögekben két-két oldal, valamint általuk bezárt szög (60°) megegyezik, így a két háromszög egybevágó egymással, amiből AD=CF is következik. Az ADC háromszöget az ABC háromszög középpontja körüli 120°-os forgatással vihetjük át a CFB háromszögbe.
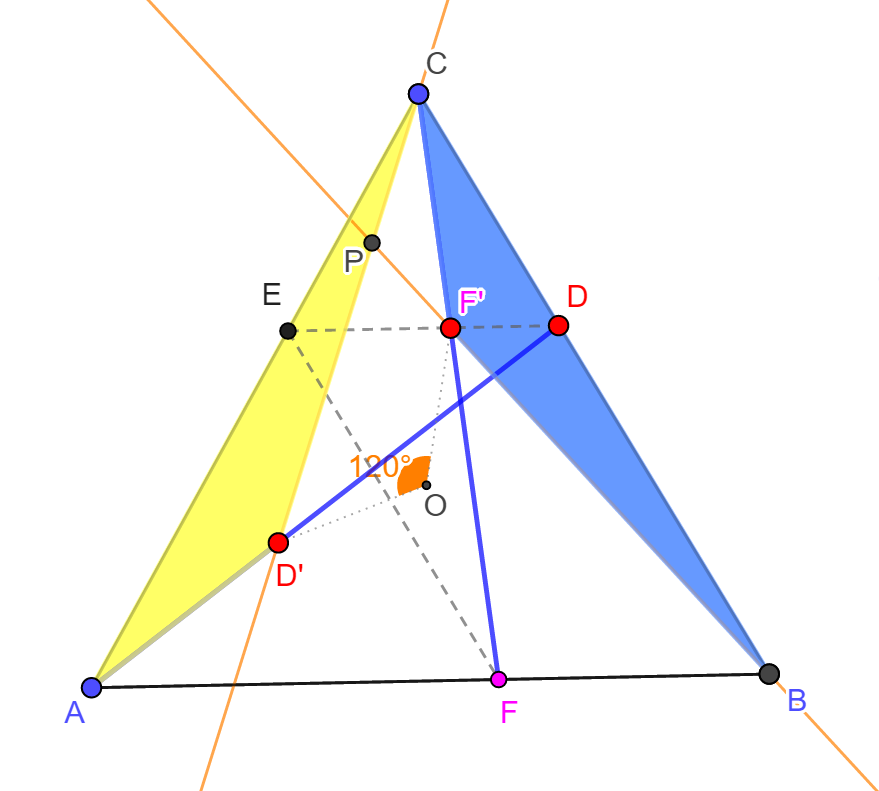
Felhasználva az 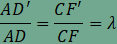 feltételt, valamint AD és CF egyenlőségét láthatjuk, hogy AD’=CF’ is teljesül. Ebből azonnal adódik, hogy az AD’C és CF’B háromszögek is egybevágók, és ugyanúgy az ABC háromszög középpontja körüli 120°-os forgatással vihető egyik a másikba. Ekkor persze az egymásnak megfelelő CD’ és BF’ egyenesek a forgatás szögét zárják be egymással, azaz ha a két egyenes metszéspontját P jelöli, akkor
és így
A
két egyenes tehát |
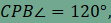
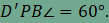
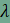értékétől
függetlenül mindig 60°-os szöget zár
be egymással.