| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
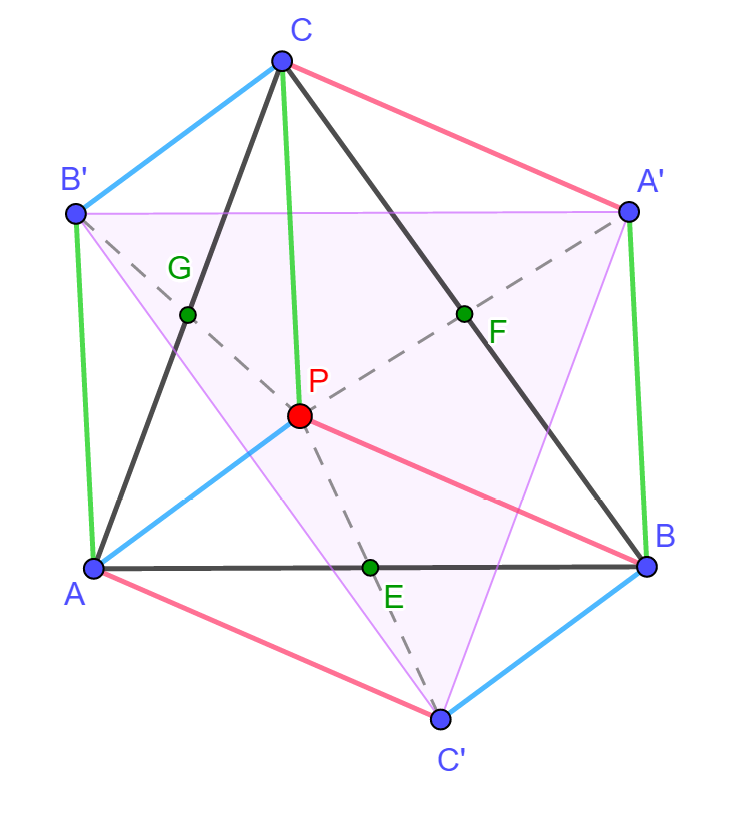
Az ABC háromszög belsejében felveszünk egy P pontot, majd tükrözzük a háromszög BC, CA, AB oldalának felezőpontjára, így rendre az A', B', C' pontokat kapjuk. Figyeljük meg az A'B'C' háromszöget a P pont különböző helyzetei mellett. Mit tapasztalunk? Milyen kapcsolat van az AA', BB', CC' szakaszok között? Magyarázzuk meg észrevételeinket! |
|
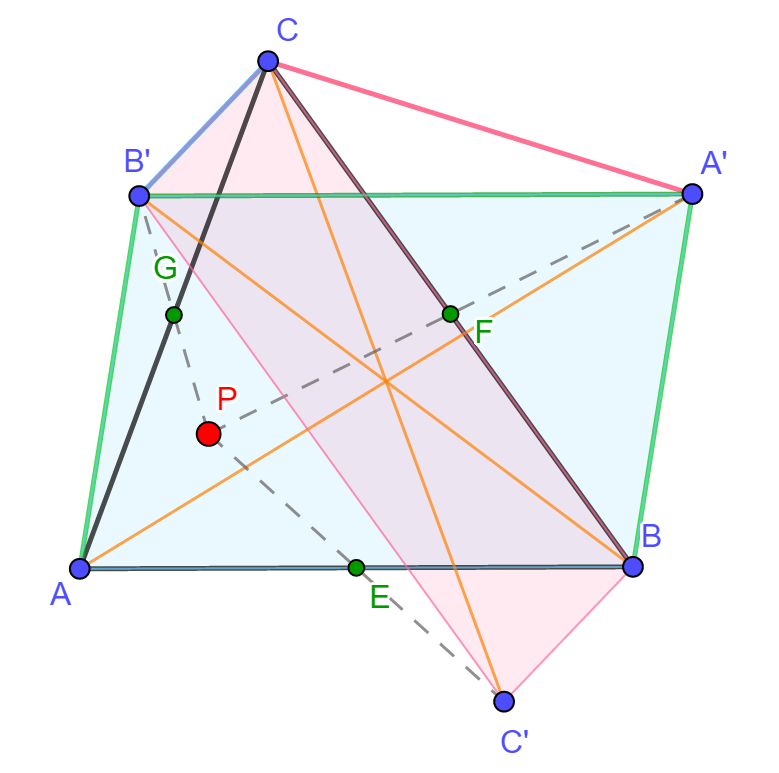
Az animáció segítségével azonnal megfogalmazható a sejtés, amely szerint az A'B'C' háromszög a P pont helyzetétől függetlenül mindig egybevágó az ABC háromszöggel, sőt a két háromszög megfelelő oldalai párhuzamosak is egymással. Az állítás igazolásához tekintsük az alábbi ábra és animáció jelöléseit. A középpontos tükrözés tulajdonságai alapján az APCB' négyszög átlói felezik egymást, ezért a négyszög paralelogramma, így AB' és PC párhuzamosak és egyenlők egymással. Szintén felezik egymást a PCA'B négyszög átlói, ezért szintén paralelogrammáról van szó, amiből adódóan PC és BA' is párhuzamos egymással és a két szakasz hossza is egyenlő. Ekkor viszont AB' és BA' egymással is párhuzamos és hosszuk is megegyezik, ezért az AB'A'B négyszög is paralelogramma, amiből következik, hogy AB és A'B' is párhuzamos és egyenlők. Az ábra további paralelogrammáit felhasználva ugyanígy bizonyítható, hogy BC és B'C', illetve CA és C'A' is párhuzamosak és egyenlők. Ebből az ABC és A'B'C' háromszögek egybevágósága már könnyen adódik.
Az
AA',
BB',
CC'
szakaszok egy
pontban metszik egymást és felezik egymást. Ehhez elegendő, ha
észrevesszük, hogy az ABA'B'
paralelogrammában AA'
és BB'
átlók, így valóban felezik egymást. A BCB'C'
paralelogramma átlói (BB'
és CC') is
felezik egymást, amit úgy is értelmezhetünk, hogy a CC' szakasz is
átmegy a BB'
és AA'
közös felezőpontján. A három szakasz valóban felezve metszi egymást.
Megjegyezzük, hogy e szakaszok közös pontja egyben annak a középpontos
tükrözésnek a középpontja is, amely az ABC és A'B'C'
háromszögeket egymásba viszi át.
|