| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
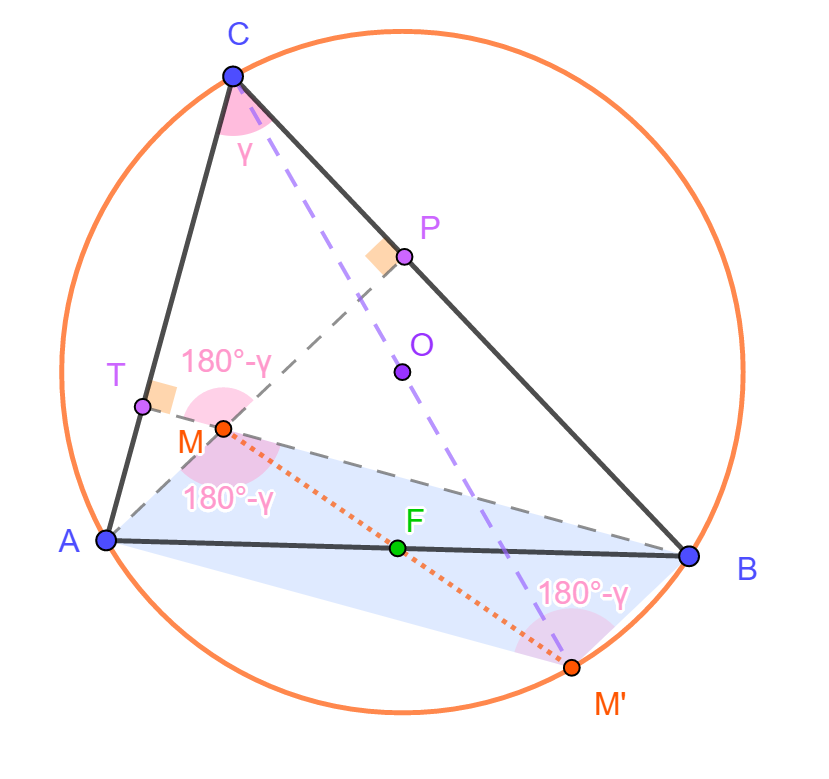
| A hegyesszögű ABC háromszög M magasságpontját tükrözzük AB oldalának F felezőpontjára! Szerkesszük meg az ABC háromszög köré írható kört! Mit tapasztalunk? Igazoljuk sejtéseinket! Vizsgáljuk meg, hogy igazak maradnak-e a sejtések, ha az ABC háromszög már nem hegyesszögű! |
|
Az animáció alapján a következő sejtések fogalmazhatók meg. Az M pont M' tükörképe illeszkedik az ABC háromszög köré írható körre, továbbá a CM' szakasz a körülírt kör egyik átmérője. Az
állítások igazolásához tekintsük az alábbi ábra és animáció jelöléseit.
A CTMP
négyszögben a T
és P
csúcsoknál derékszögek vannak, így húrnégyszögről van szó. Ekkor
viszont ha az ABC
háromszög C
csúcsánál Most megmutatjuk, hogy ebben a körben a CM' szakasz átmérő. Valóban, mivel az AM'BM négyszög paralelogramma (átlói felezik egymást), ezért BT és M'A párhuzamosak egymással. Mivel BT merőleges az AC oldalra, ezért a vele párhuzamos M'A szintén merőleges AC-re. Ez azt jelenti, hogy a CAM' háromszög derékszögű, ezért CM' átfogója valóban átmérő a háromszög köré írható körben.
Az
animáció segítségével
meggyőződhetünk arról, hogy állításaink nem csak hegyesszögű
háromszögben, hanem minden háromszögben érvényesek. Ennek bizonyítása
derékszögű és tompaszögű háromszögre a fentiekhez hasonlóan, a
megfelelő húrnégyszögek megtalálásával könnyen elvégezhető.
|
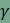szög
van, akkor 
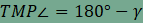. Ez
utóbbi szögnek 
csúcsszöge, ezért 
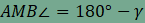is
teljesül. A középpontos tükrözés szögtartó tulajdonsága miatt
pedig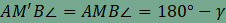 
, és így a 