| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
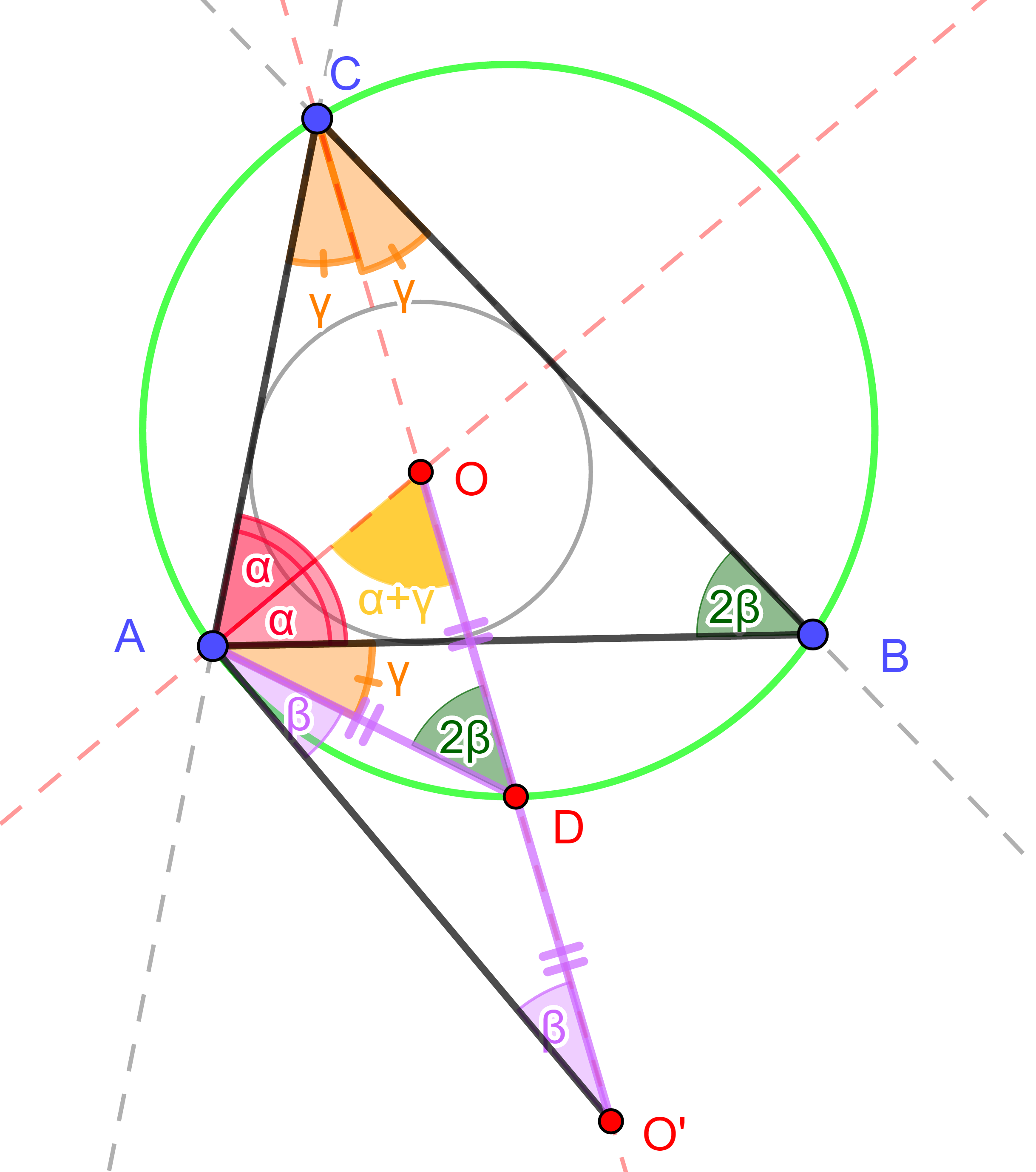
| Az ABC háromszög beírt körének O középpontját tükrözzük a C csúcsból induló (belső) szögfelező, és a háromszög köré írt kör C-től különböző D metszéspontjára. A háromszög melyik nevezetes pontja lesz a kapott O' pont? Indokoljuk meg sejtésünket! |
|
Az animáció segítségével meggyőződhetünk arról, hogy az O' pont az ABC háromszög AB oldalához írt kör középpontja. Ez a kör érinti az ABC háromszög AB oldalát, valamint AC és BC oldalegyeneseit. A sejtés bizonyításához megmutatjuk, hogy az O' pont illeszkedik az ABC háromszög A csúcsánál lévő külső szögfelezőjére. Az ismertetett bizonyításhoz hasonlóan megmutatható, hogy O' a B csúcsnál lévő külső szögfelezőnek is pontja, és mivel a konstrukcióból adódóan az A csúcsnál lévő belső szögfelezőn is rajta van, ezért valóban csak az AB oldalhoz írt kör középpontja lehet. Jelölje
az ABC
háromszög belső szögeit A
középpontos tükrözés miatt azonban OD=O'D, amiből
következik, hogy az AO'D
háromszög is egyenlőszárú, ezért az AO' alapon fekvő
szögei megegyeznek. E szögek összege azonban megjelenik a D csúcsnál lévő
külső szögnél is, vagyis a szögek összege
|
 .
Ekkor
.
Ekkor 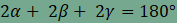 . Először
megmutatjuk, hogy az
. Először
megmutatjuk, hogy az 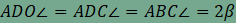 adódik. Másrészt
adódik. Másrészt 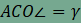 és
és 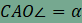 , így a háromszög
, így a háromszög 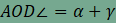 . A kerületi szögek
tétele szerint a
. A kerületi szögek
tétele szerint a 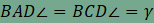 , és így az
, és így az 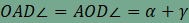 , azaz a háromszög
valóban egyenlőszárú és
, azaz a háromszög
valóban egyenlőszárú és  , így
, így 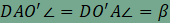 . Most már
láthatjuk, hogy
. Most már
láthatjuk, hogy 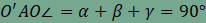 . Ez
azt jelenti, hogy
. Ez
azt jelenti, hogy