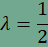| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
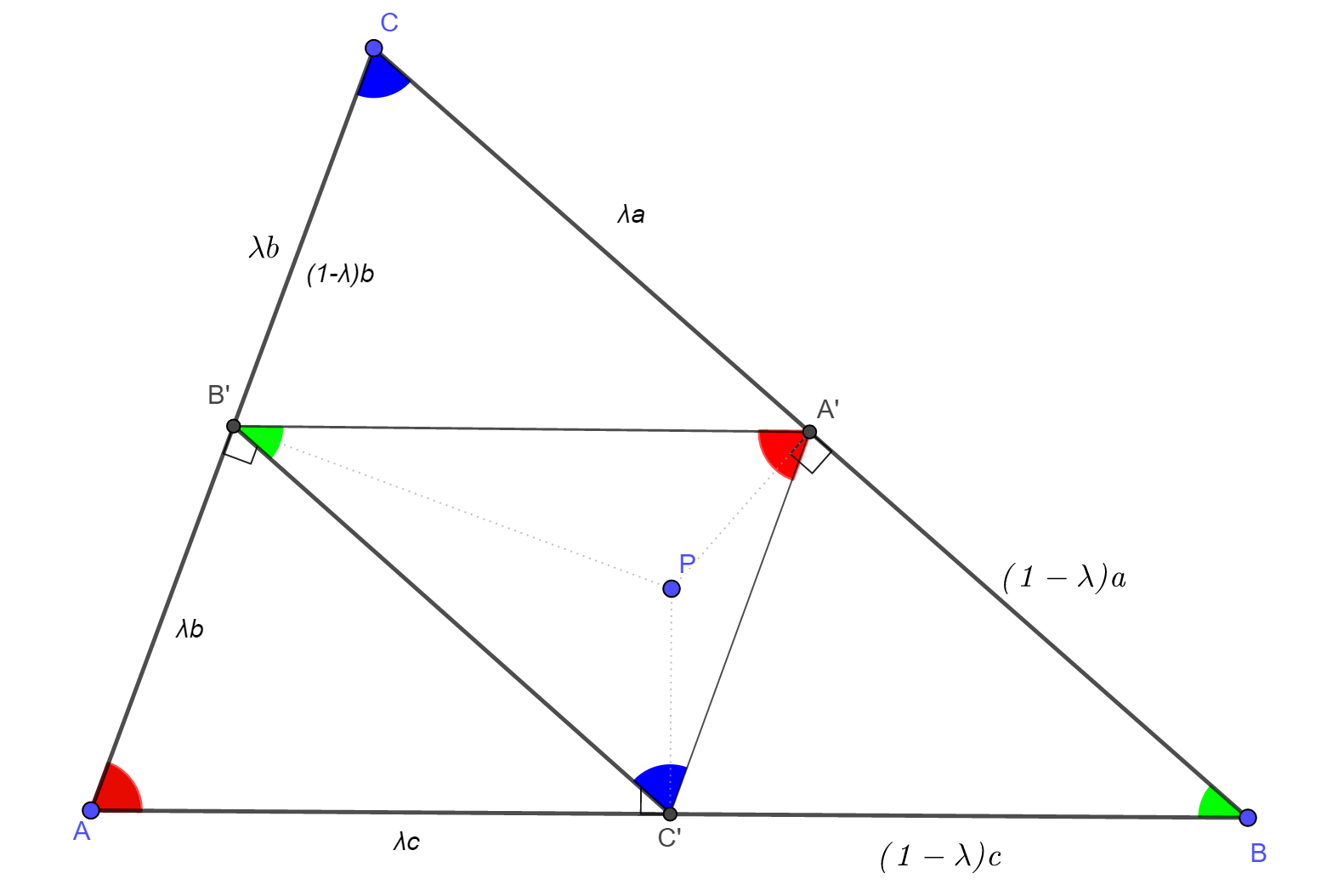
Az
ABC
hegyesszögű
háromszög egy belső pontja P, a P pont BC,
BA és CA
oldalakra eső merőleges vetülete
rendre A’, C’
és B’. Határozzuk meg
az összes olyan P pontot, amelyre 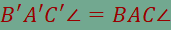 és és 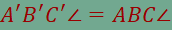 feltételek
teljesülnek! feltételek
teljesülnek! |
|
Póta Balázs, a Révai Miklós Gimnázium 12. osztályos tanulójának megoldása Az ABC háromszög szögeit a szokásos módon jelöljük. Tükrözzük az A'B'C' háromszöget a B'C' oldal felezőpontjára, a tükörképet jelöljük Q-val. A tükrözés szögtartó tulajdonsága miatt
Vegyük észre, hogy az AC’PB’ négyszögben a B’ és C’ csúcsoknál derékszögek vannak, ezért a négyszög húrnégyszög. Ebből adódik, hogy
Vizsgáljuk
meg a QC’A’B’
négyszöget! Ebben az A’ és Q csúcsoknál lévő szögek összege 180°,
így a négyszög húrnégyszög. Ez azt is jelenti, hogy a P
pont E-re
vonatkozó
tükörképe illeszkedik az A’B’C’
háromszög köré írható körre.
Ugyanígy beláthatjuk, hogy ha a P pontot az A’C’ oldal F, vagy az A’B’ oldal G felezőpontjára tükrözzük, akkor olyan R, S pontokhoz jutunk, amelyek szintén illeszkednek az A’B’C’ háromszög körülírt körére, azaz a P pontnak mindhárom oldal felezőpontjára vonatkozó tükörképe rajta van az A’B’C’ háromszög köré írható körén. Ismert, hogy a háromszög magasságpontja rendelkezik ezzel a tulajdonsággal, ezért a P pont lehet az A’B’C’ háromszög magasságpontja. Más pont viszont nem lehet.
Ennek igazolásához tekintsünk egy P
pontot, amelyik illeszkedik a B’C’
szakasz az
A’C’
szakasz lehet. Ezek közül egyik a C’ pont, a másik az A’B’C’ háromszög magasságpontja. Ebből valóban következik, hogy más pont nem jöhet szóba. Eddigi gondolatmenetünk alapján P az A’B’C’ háromszög magasságpontja, ezért az A’P, B’P és C’P egyenesek a háromszög magasságvonalai. Ebből azonnal következik, hogy A’B’ és AB, B’C’ és BC, valamint C’A’ és CA párhuzamosak egymással. Ekkor viszont az A’B’C és a BAC háromszögek hasonlók
egymáshoz, ha hasonlóságuk arányát 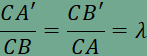 . .
Az A’C’B háromszög is hasonló az CAB háromszöghöz, továbbá hasonlóságuk aránya
ezért 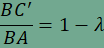 is teljesül. Végül AC’B’ háromszög is hasonló ABC háromszöghöz, és hasonlóságuk aránya 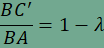 , ,
ezért 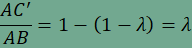 . .A már ismert gondolatmenettel láthatjuk, hogy 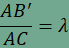 , ,és
így egybe, ezért P csak az ABC háromszög köré írt kör középpontja lehet.
|
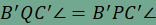
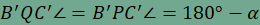
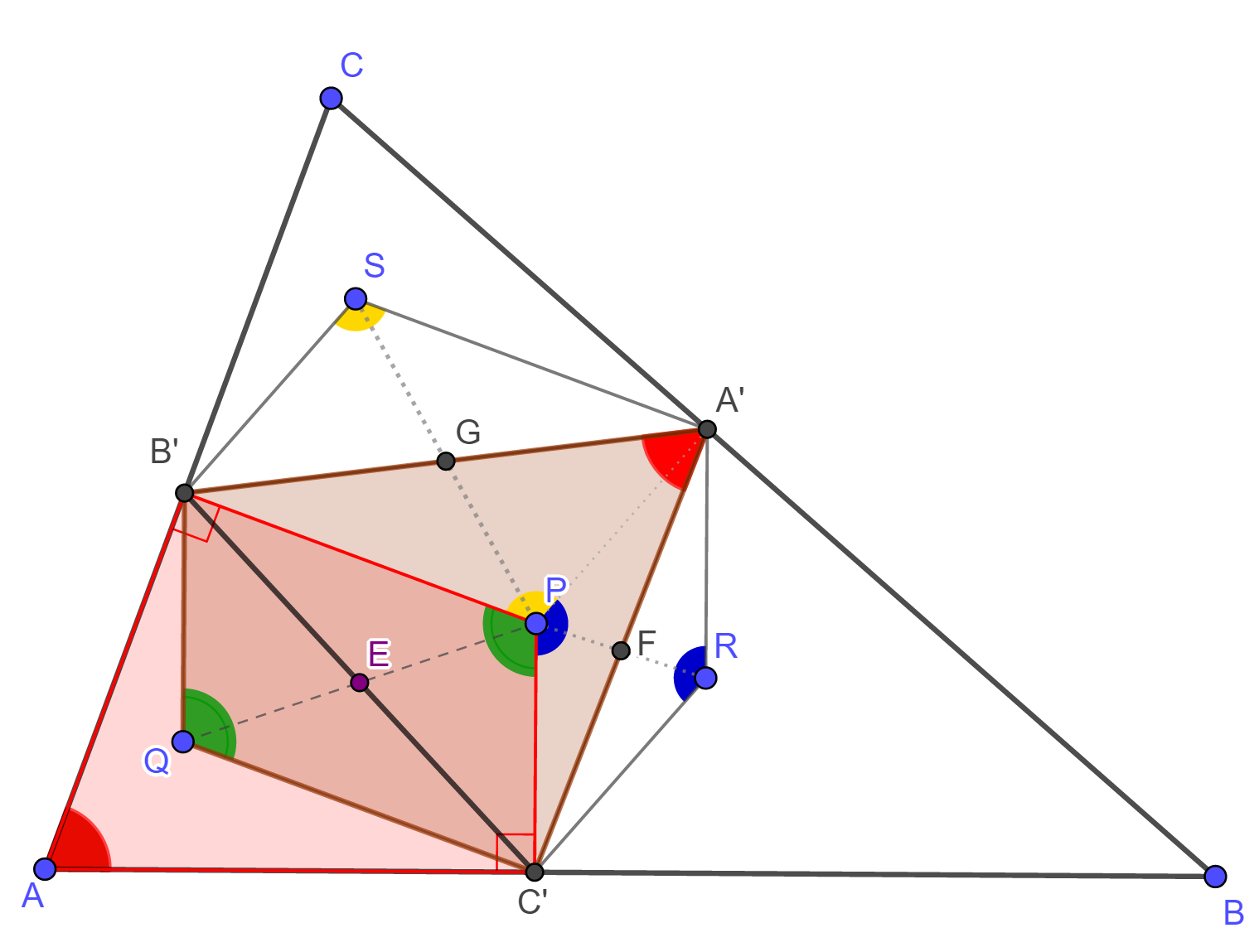
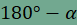
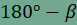
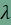
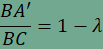 ,
,