Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
| Pitagorasz-tétele
I. Az alábbi animáció segítségével emeljünk négyzeteket a derékszögű háromszög oldalaira. Bizonyítsuk be, hogy a két befogóra emelt négyzet területének összege megegyezik az átfogóra emelt négyzet területével. |
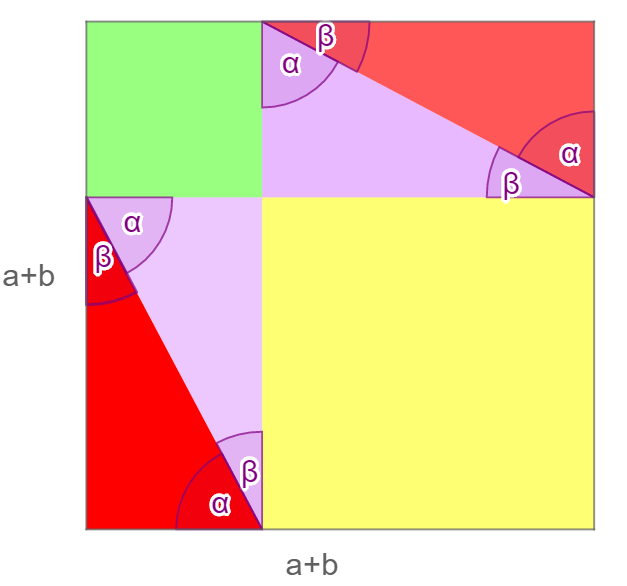
Az animációban lépésről lépésre követhető, hogy miként építhetünk a derékszögű háromszöggel egybevágó háromszögekből, valamint az oldalakra rajzolt négyzetekből egy-egy nagyobb négyzetet.Az első négyzetben (az n csúszkával felépíthető) előbb a derékszögű háromszög (lila) befogóira emeltünk négyzeteket (zöld és sárga), majd a két négyzet egy-egy oldalához egy, az eredeti derékszögű háromszöggel egybevágó háromszöget (a másik lila) illesztettünk. Végül a két lila háromszög átfogójához egy-egy további, velük egybevágó háromszöget (piros színnel) illesztettünk. Ha a derékszögű háromszög hegyesszögeit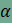 és és 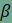 jelölik,
akkor az ábrán azonos módon jelölt szögek egymással megegyeznek. Mivel jelölik,
akkor az ábrán azonos módon jelölt szögek egymással megegyeznek. Mivel
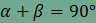 , ezért a színes síkidomok együtt egy négyzetet alkotnak, amelynek
oldala pont a derékszögű háromszög két befogójának összege (az
ábrán , ezért a színes síkidomok együtt egy négyzetet alkotnak, amelynek
oldala pont a derékszögű háromszög két befogójának összege (az
ábrán 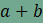 ).
Ha a derékszögű háromszög területét T jelöli, akkor a nagy négyzet
területe ).
Ha a derékszögű háromszög területét T jelöli, akkor a nagy négyzet
területe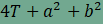 . .
Most
nézzük az m csúszkával felépíthető négyzetet! Itt előbb a derékszögű
háromszög (lila) átfogójára emeltünk egy négyzetet (kék
színnel), majd ennek további oldalaihoz, mint átfogókhoz illesztettünk
egy-egy, az eredetivel egybevágó derékszögű háromszöget (a további lila
háromszögek). Az egybevágóság miatt az ahol c a derékszögű háromszög átfogóját jelöli.
Az 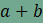 oldalú négyzet
területére kapott összefüggések alapján oldalú négyzet
területére kapott összefüggések alapján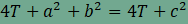 , ,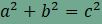 . . |
 . Ebből adódóan a "szomszédos" lila
háromszögek megfelelő befogói egy egyenesre illeszkednek, így az
"építkezés" után valójában ismét egy
. Ebből adódóan a "szomszédos" lila
háromszögek megfelelő befogói egy egyenesre illeszkednek, így az
"építkezés" után valójában ismét egy 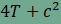 ,
,