Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
| Pitagorasz-tétele
II. Az alábbi animáció segítségével emeljünk négyzeteket a derékszögű háromszög oldalaira. Bizonyítsuk be, hogy a két befogóra emelt négyzet területének összege megegyezik az átfogóra emelt négyzet területével. |
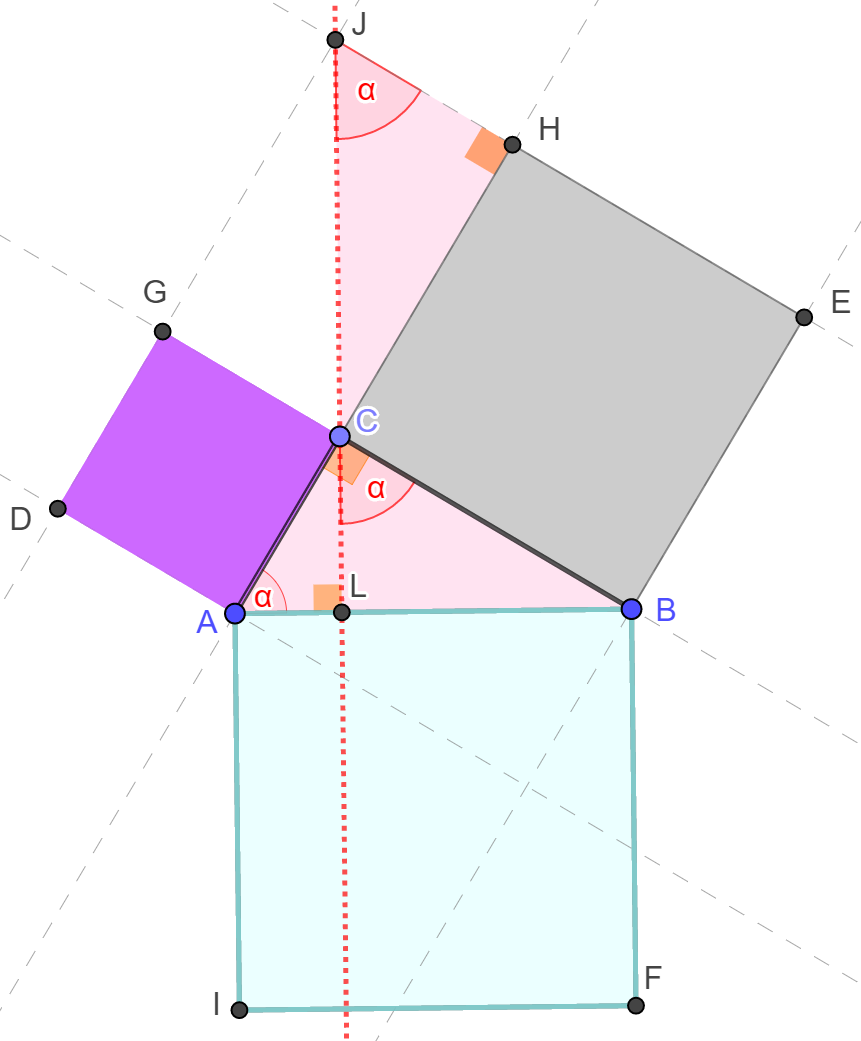
Az
ABC
derékszögű háromszög AC
és BC
befogóira kifelé az ACGD
és a BCHE,
átfogójára az ABFI
négyzetet emeltük az ábra szerint. Az átfogóhoz
tartozó magasságvonal talppontja L,
a magasságvonal az EH
egyenest a J
pontban metszi. Ha
|
 |
| Az animáció indítása |
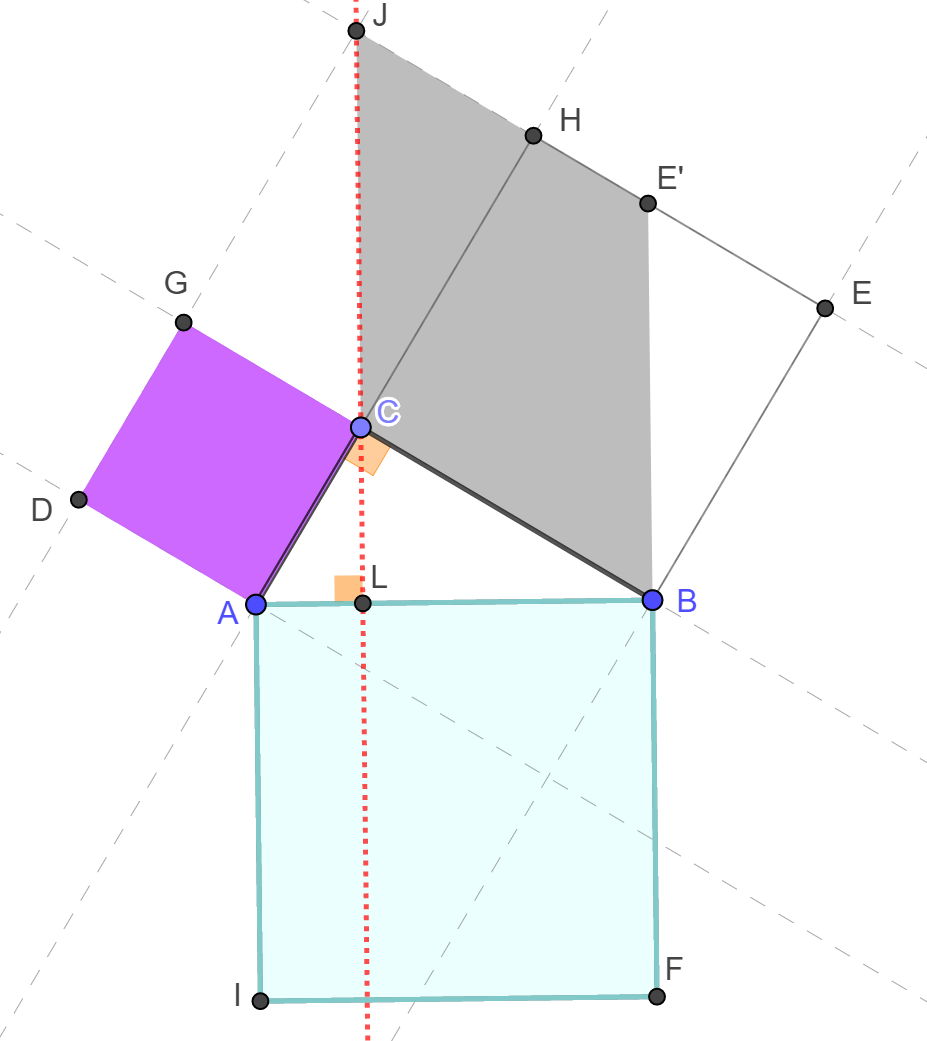
A fenti észrevételek birtokában "döntsük meg" a CBEH négyzetet úgy, hogy CB oldalát fixen hagyjuk, HE oldalát pedig ezzel párhuzamosan változtatjuk, figyelve arra, hogy a négyszög a transzformáció során végig paralelogramma maradjon (Szürke síkidom 1. lépés csúszka). A transzformáció után a CBE'J paralelogrammát kapjuk. Az átalakítás legfontosabb tulajdonsága, hogy közben a paralelogramma területe végig ugyanakkora, pontosan megyezik a CBEH négyzet területével, hiszen a CB alap nem változott, és nem változott az ehhez az oldalhoz tartozó magasság sem, mert HE végig a CB-vel párhuzamos egyenesen mozgott. Eszerint a CBE'J paralelogramma területe ugyanakkora, mint a CBEH négyzet területe. Vegyük még észre, hogy a paralelogramma szemközti oldalai egyenlők, ezért E'B=CJ=AB.
 |
| Az animáció indítása |
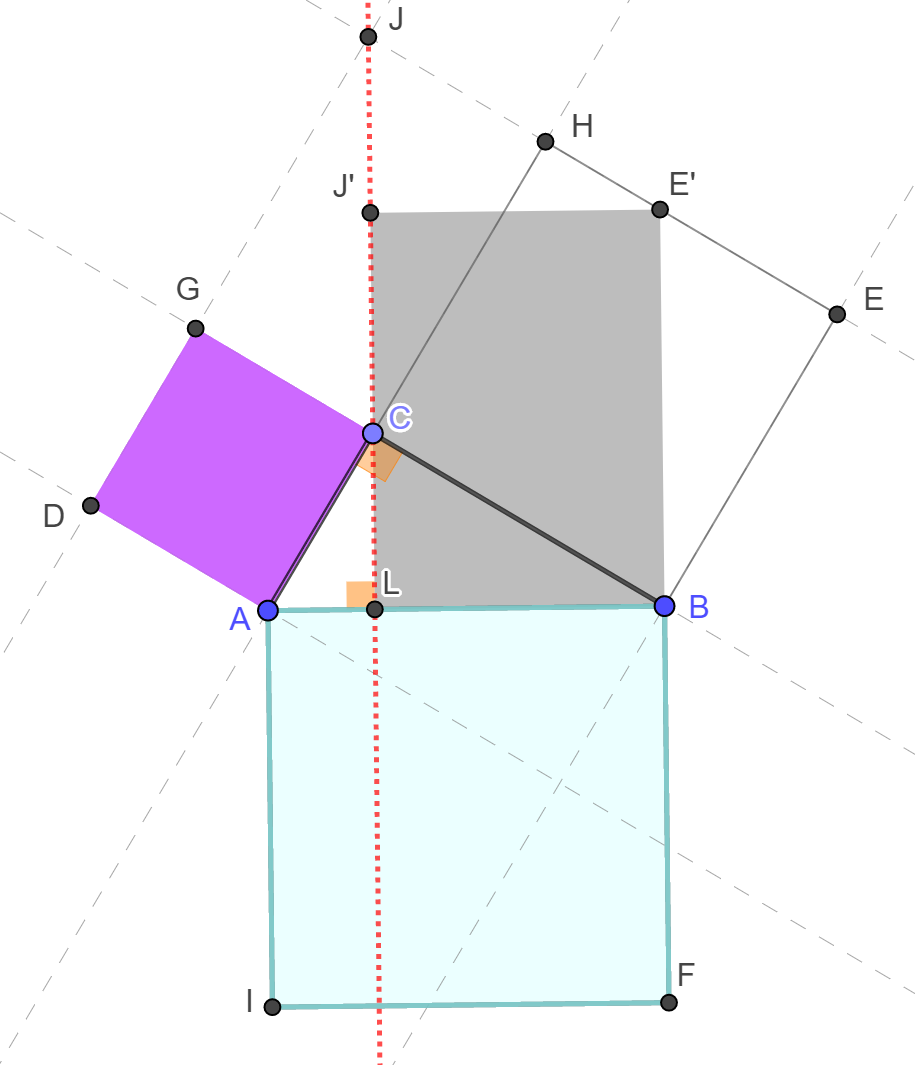
A Szürke síkidom 2. lépés csúszka segítségével a CBE'J paralelogrammát "döntjük" úgy, hogy E'B=AB oldalát fixen hagyjuk, és figyelünk arra, hogy a transzformáció során végig paralelogramma maradjon. A transzformáció végén az LBE'J' téglalapot kapjuk. A téglalap területe tehát ugyanakkora, mint a CBE'J négyszög területe, ami pedig ugyanakkora, mint a CBEH négyzet területe. Az LBE'J' téglalap oldalai LB és E'B=CB.
 |
| Az animáció indítása |
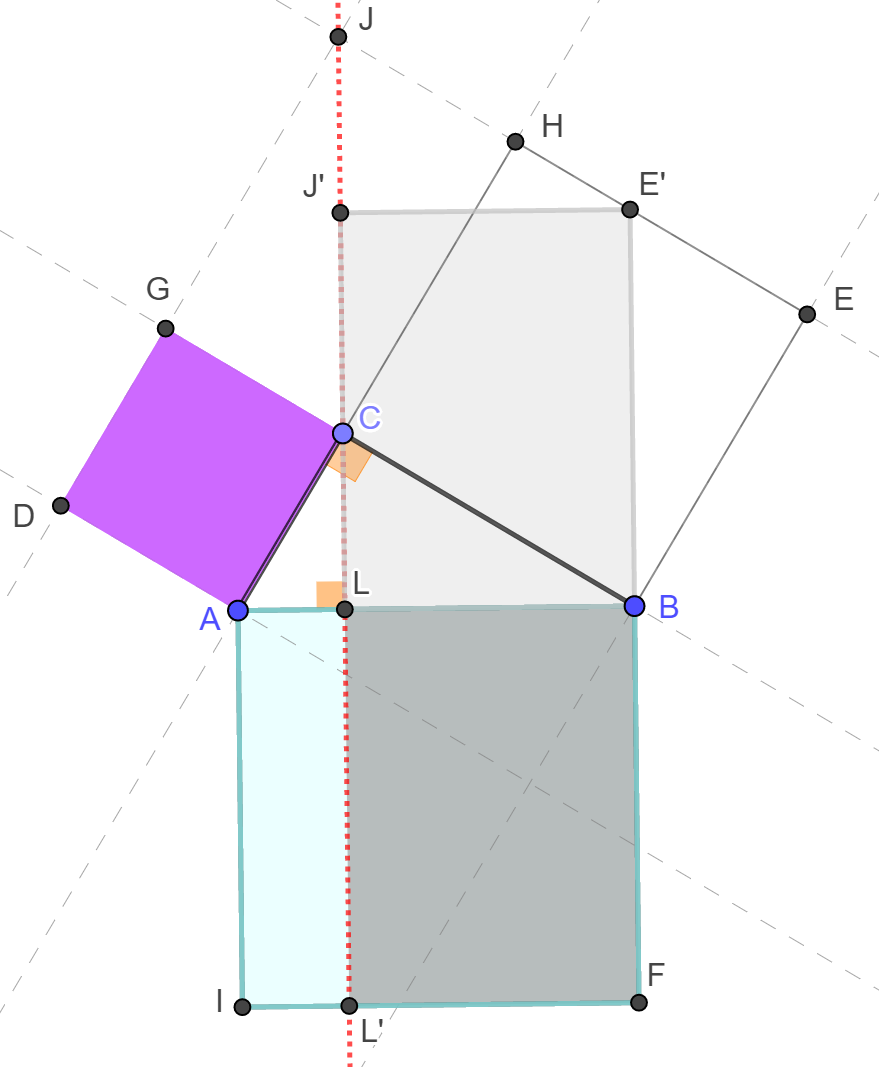
Az LBE'J' téglalap oldalai ezek szerint ugyanakkorák, mint az alábbi ábrán szereplő L'FBL téglalap oldalai. Ez azt is jelenti, hogy az előbbi téglalap egy eltolással az utóbbi téglalapba vihető, eközben nyilván nem változik meg a területe (Szürke síkidom 3. lépés).
 |
| Az animáció indítása |
A CBEH négyzet területe tehát ugyanakkora, mint az L'FBL téglalap területe. Hasonló gondolatmenet mutatja, hogy az ACGD négyzet területe megegyezik az IL'LA téglalap területével. Ezzel Pitagorasz-tételét bebizonyítottuk.
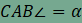 ,
akkor
,
akkor 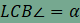 is teljesül,
hiszen a két szög merőleges szárú szögpárt alkot. Ekkor
viszont
is teljesül,
hiszen a két szög merőleges szárú szögpárt alkot. Ekkor
viszont 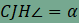 ,
hiszen
,
hiszen 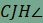 és
és 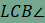 egyállású szögek.
Így
viszont az
egyállású szögek.
Így
viszont az