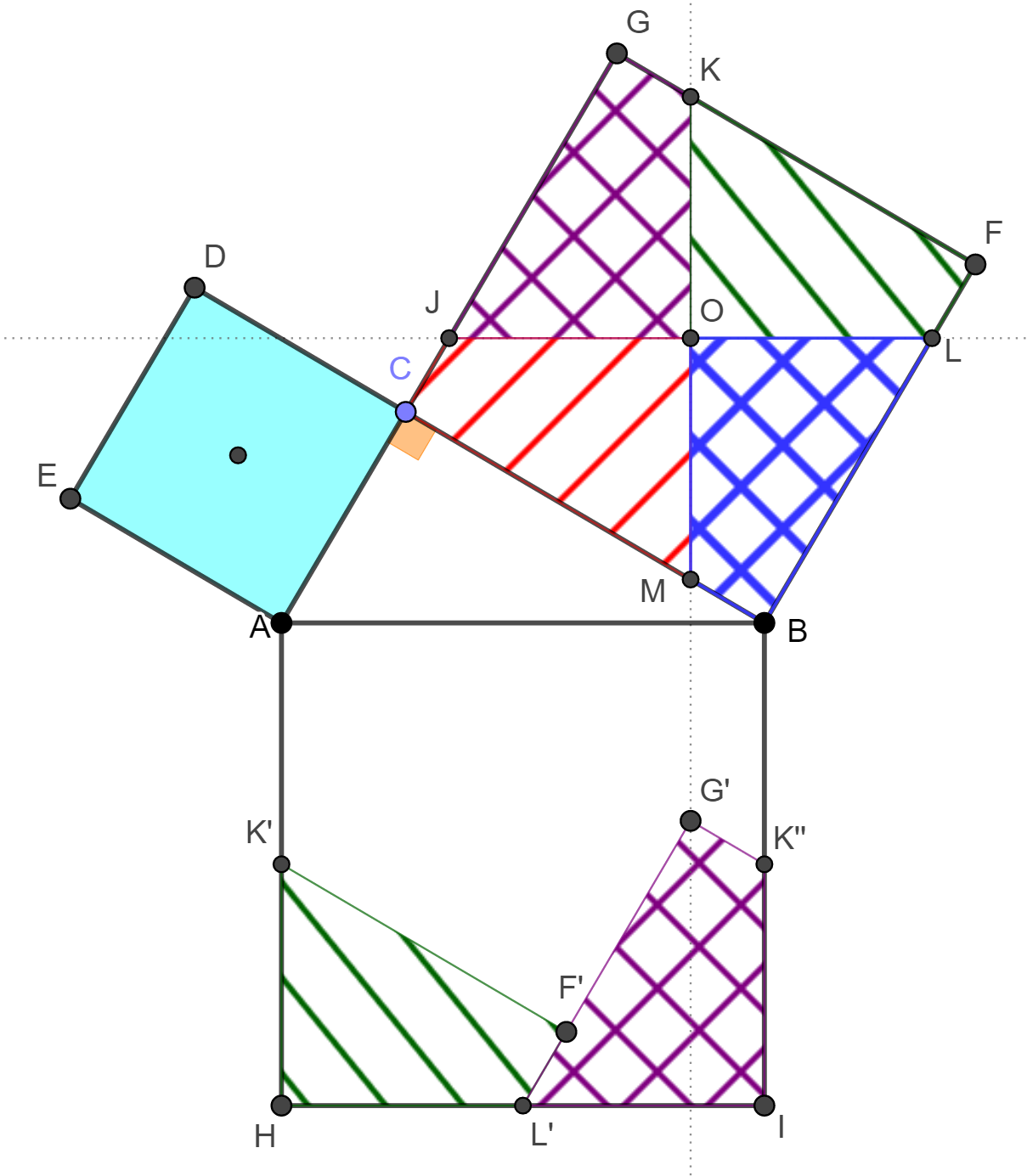
Az ABC derékszögű háromszög AC és BC befogóira kifelé az ACDE és a BCGF, átfogójára az ABIH négyzetet emeltük az ábra szerint. A hosszabb átfogóra emelt négyzet O középpontján keresztül húzott vágások a BCGF négyzetet az ábra szerint 4 részre bontják. Először vegyük észre, hogy a kapott részek egymással egybevágók, hiszen pl. az O pont körüli 90°-os forgatás az MBLO négyszöget az LFKO négyszögbe viszi (a négyzet és a két vágás alkotta alakzat invariáns a forgatásra nézve). Az MBLO négyszöget tovább forgatva újabb 90° után a KGJO, majd a JCMO négyszöget kapjuk, amint arról az alábbi animáció segítségével is meggyőződhetünk. 

Az animáció indítása

A következőkben toljuk el az OLFK négyszöget úgy, hogy az O csúcs a H csúcsba kerüljön! Mivel OK párhuzamos HA-val, ezért az eltolás után a K pont K' képe illeszkedik a HA szakaszra, és ehhez hasonlóan az L pont L' képe illeszkedik a HI szakaszra. Ezután toljuk el az OKGJ négyszöget úgy, hogy az O pont képe I legyen. Ugyanolyan megfontolásból a K pont K'' képe IB-re, a J pont képe (J') pedig IH-ra esik.

Megmutatjuk, hogy a J pont képe egybeesik L'-vel és F' illeszkedik a JG szakasz eltolt képére (L'G'-re). Ehhez vegyük észre, hogy ABLJ paralelogramma, ezért

 ,

,

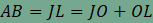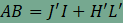és mivel JO=J'I és OL=HL', így 

, 

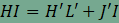amiből HI=AB miatt 

,

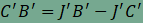 ami csak úgy képzelhető el, ha J' és L' egybeesik. Másrészt LF és JG párhuzamosak, ezért eltolt képeik, L'F' és L'G' is párhuzamosak. Ebből valóban következik, hogy F' illeszkedik L'G'-re. Eredményeinket úgy is megfogalmazhatjuk, hogy az eltolt négyszögek az L' csúcsnál hézag és átfedés nélkül illeszkednek egymáshoz.

Az animáció indítása

Az alábbi ábra azt mutatja, hogy a nagyobb befogóra rajzolt négyzet további két négyszöge is eltolható az átfogóra rajzolt négyzet megfelelő csúcsaihoz, az illeszkedés mindenhol átfedés és hézag nélküli. Ez pontosan úgy bizonyítható, mint az előbb. Az ABIH négyzet "közepén" kimarad egy négyszög, az ábrán B'F'G'C' négyszög. Az eltolásokból adódóan ennek szomszédos oldalai merőlegesek (pl. J'B' párhuzamos LB-vel és C'K'' párhuzamos CB-vel, de LB és AB merőlegesek egymásra). 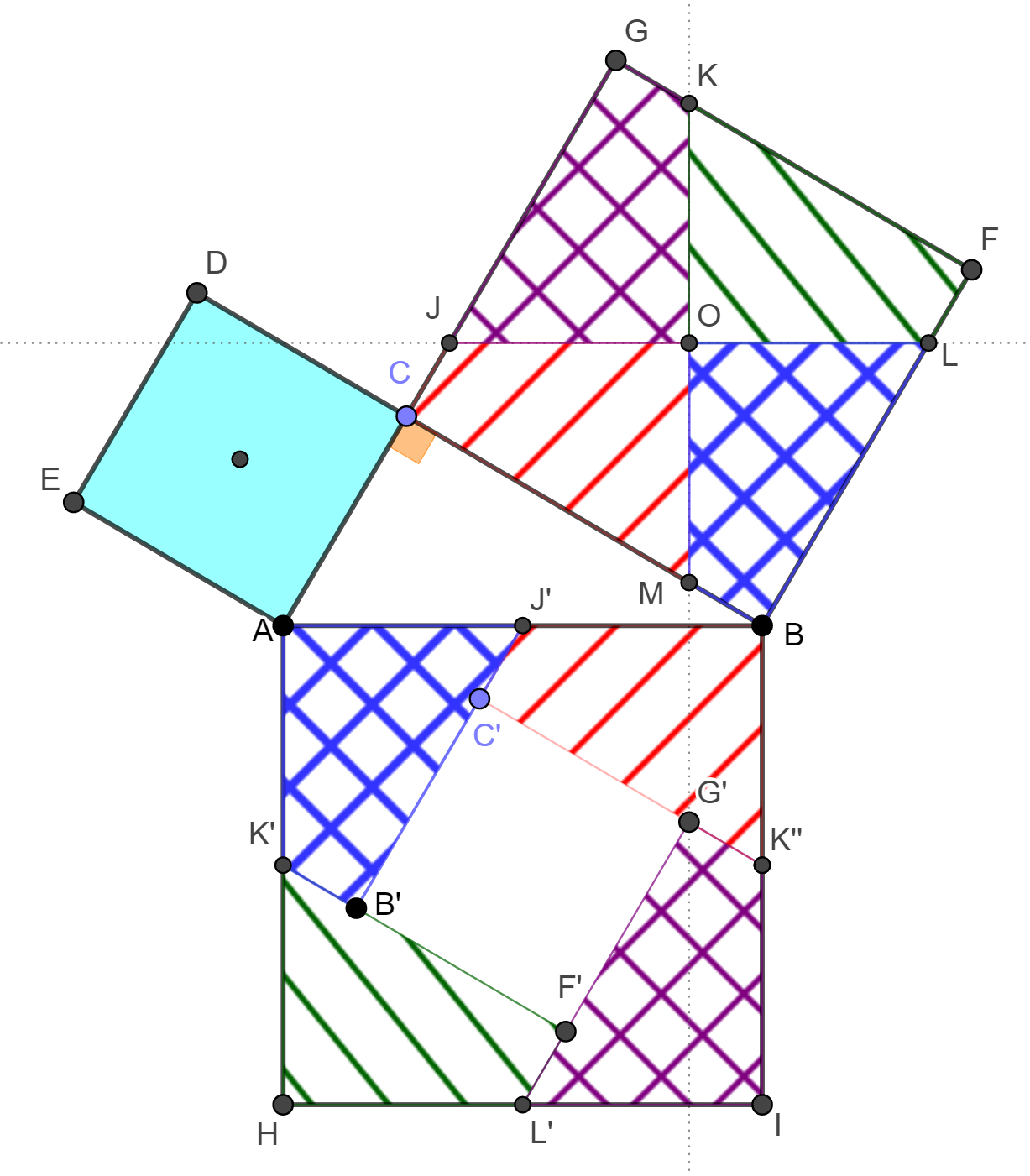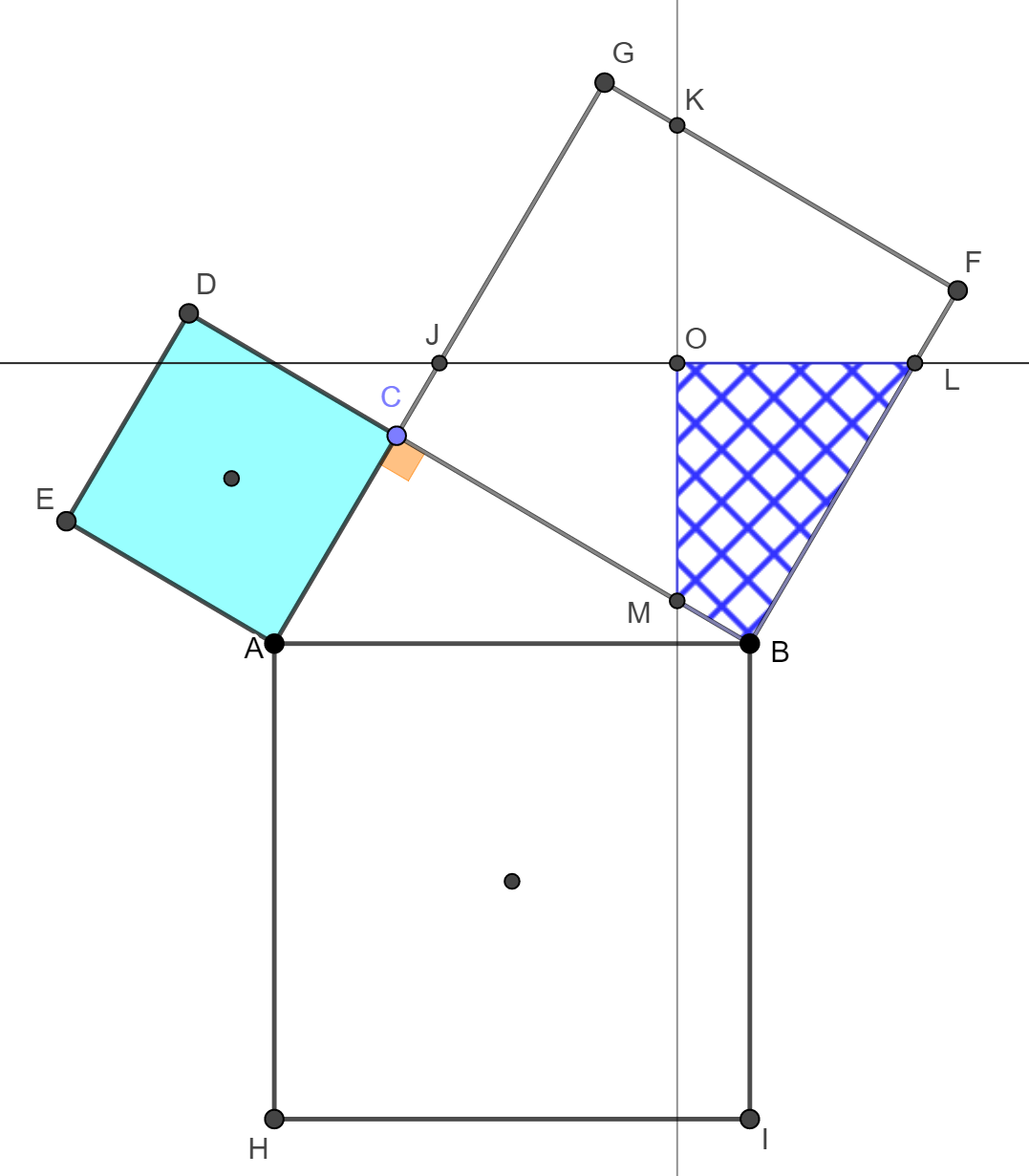A B'F'G'C' négyszög tehát téglalap, melynek oldalai párhuzamosak az ACDE négyzet megfelelő oldalaival, C'B' oldalára pedig

,

.

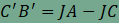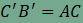Hasonló gondolatmenet mutatja, hogy a téglalap másik oldala is megegyezik az ACDE négyzet oldalával, vagyis B'F'G'C' négyzet, mely egybevágó az ACDE négyzettel. Mivel megfelelő oldalaik párhuzamosak, ezért az ACDE négyzet eltolással vihető az B'F'G'C' négyzetbe.  Ezzel az átdarabolás, és így Pitagorasz-tételének helyességét is igazoltuk.

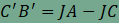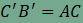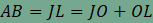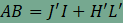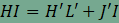Az animáció indítása