| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
Keressük
meg a sík összes olyan síkkitöltését, amely a
következő feltételeknek eleget tesz!
|
|
Egy korábbi feladatban megvizsgáltuk azokat a síkkitöltéseket, amelyek csak egyfajta szabályos sokszöget használnak. Ilyenből 3 féle létezik: ezek szabályos háromszögekből, négyszögekből vagy hatszögekből építkeznek. Ha legalább kétfajta szabályos sokszöget használunk, akkor egy csúcsnál legalább 3, legfeljebb 5 szabályos sokszög érintkezhet. Valóban, hiszen a szabályos sokszögek közül a háromszögnek a legkisebb a belső szöge (60°), ebből pedig pontosan 6 darab kell egy hézagok és átfedések nélküli lefedéshez, ezért 6 sokszögnél több semmiképpen nem vehet részt a kitöltésben. Pontosan 6 sokszög is csak akkor, amikor szabályos háromszögekből építkezünk. A másik oldalról viszont: a csomópontoknál két sokszög nyilván nem elegendő, hiszen minden szabályos sokszög konvex, ezért a szögei 180°-nál kisebbek, így két sokszög hézagmentesen nem tudja egyetlen csomópontnál sem kitölteni a síkot.
Ebben a feladatban azokat a kitöltéseket keressük, amelyeknél minden
csomópontnál 3 sokszög találkozik. Legyen
az egy csúcsnál találkozó sokszögek oldalainak száma n,
m
és k
A
csomópontoknál a kitöltés nem tartalmaz sem hézagot sem
átfedést, ezért
amiből összevonás, rendezés és
egyszerűsítés után
Ha most
ami ellentmond a fenti egyenlőségnek.
Ebből adódóan n
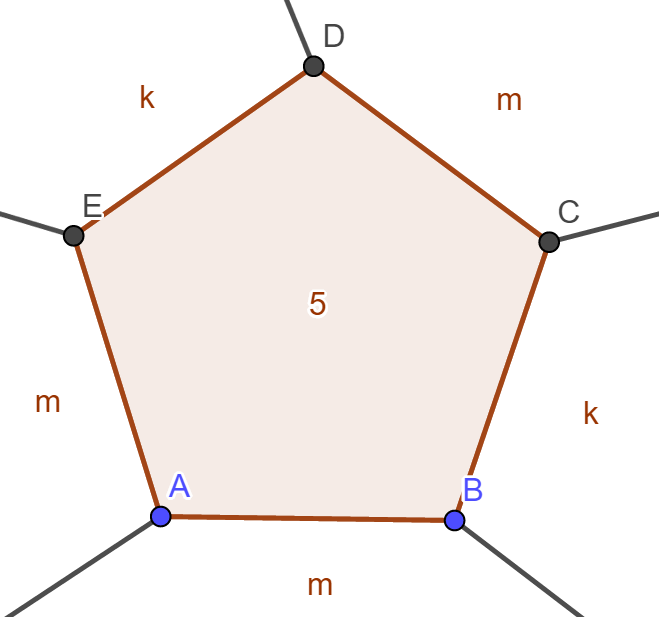
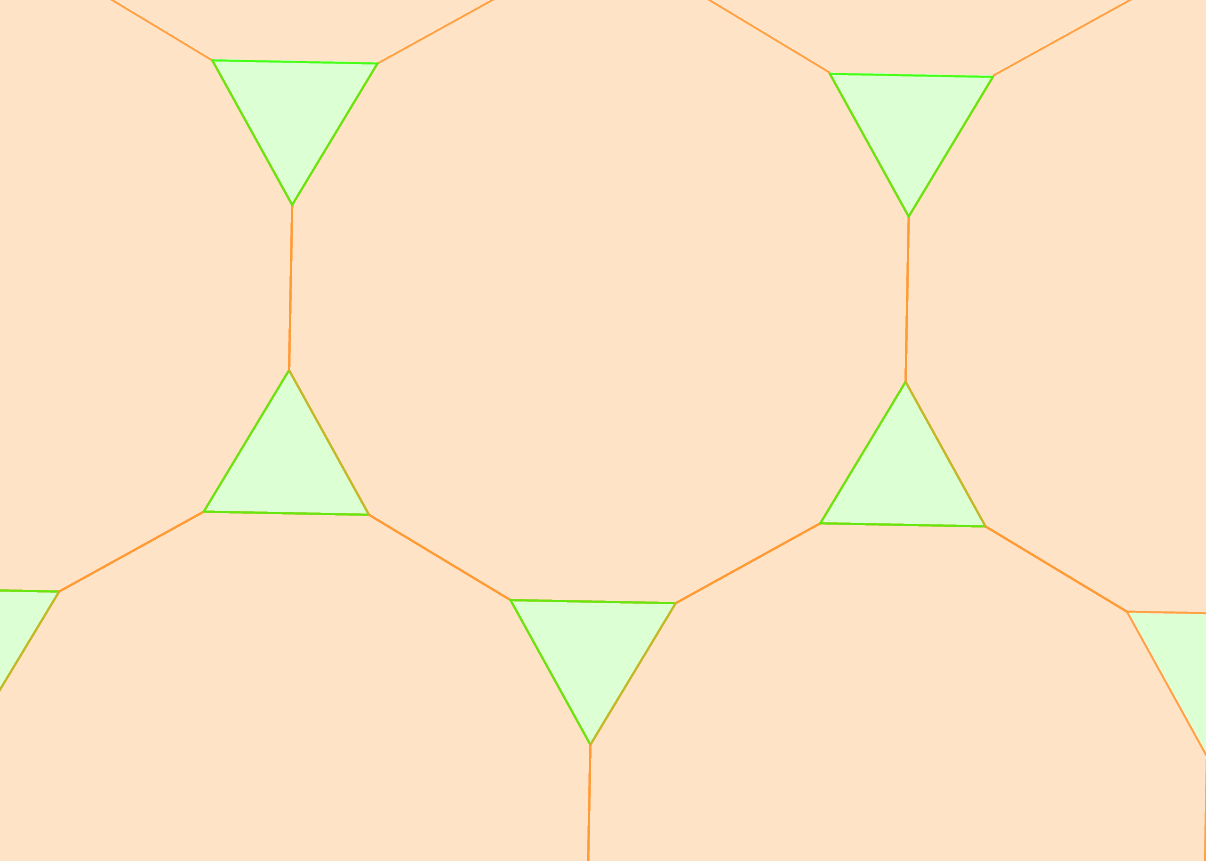
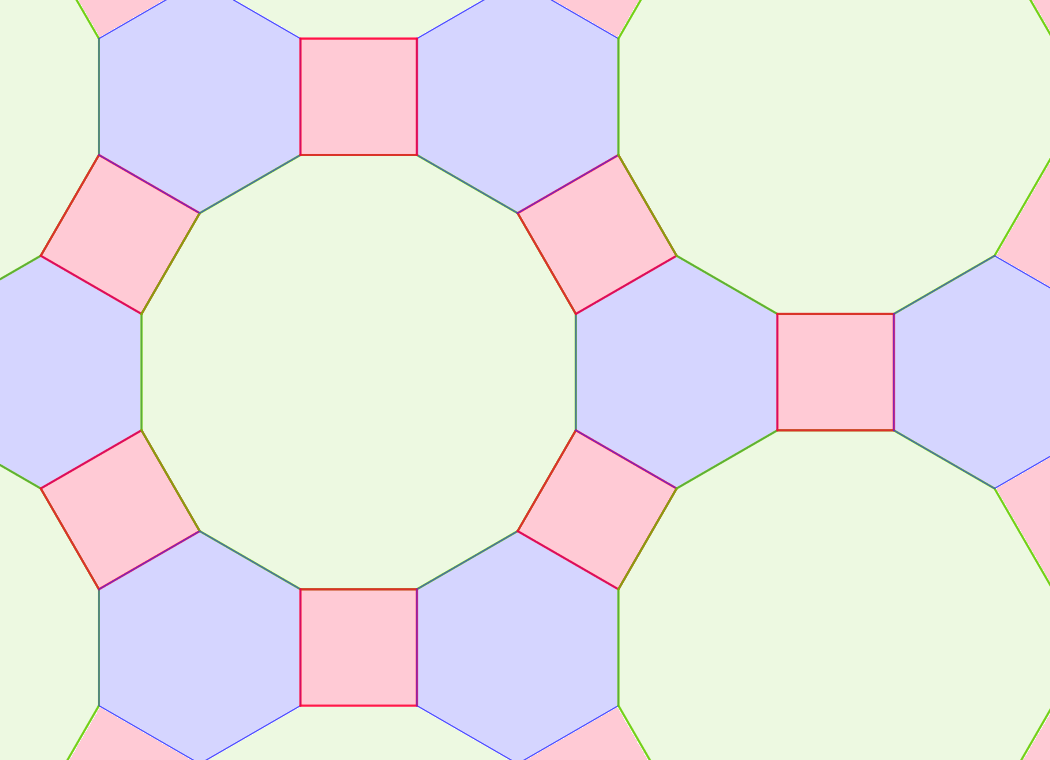
értéke 3, 4, 5 vagy 6. Vizsgáljuk meg a kitöltésben szereplő n-szöget. Ha n páratlan (az alábbi ábrán n=5, de a gondolatmenet n=3 esetén is érvényes), akkor az n-szög oldalaihoz (az AB oldaltól indulva) rendre egy m, majd egy k oldalú sokszög csatlakozik, végül az A csúcsnál két m oldalú sokszöget találunk. Ebből következik, hogy ha n páratlan, akkor m=k.
Ha n=3, akkor
aminek
egyetlen megoldása m=12.
Ebből a
(3, 12, 12) kitöltést kapjuk (a csomópontokban egy szabályos háromszög,
valamint két szabályos 12-szög találkozik). Az alábbi animáció mutatja,
hogy ez
meg is valósítható.
Ha
n=5,
akkor
aminek
nincsen egész megoldása. Vizsgáljuk
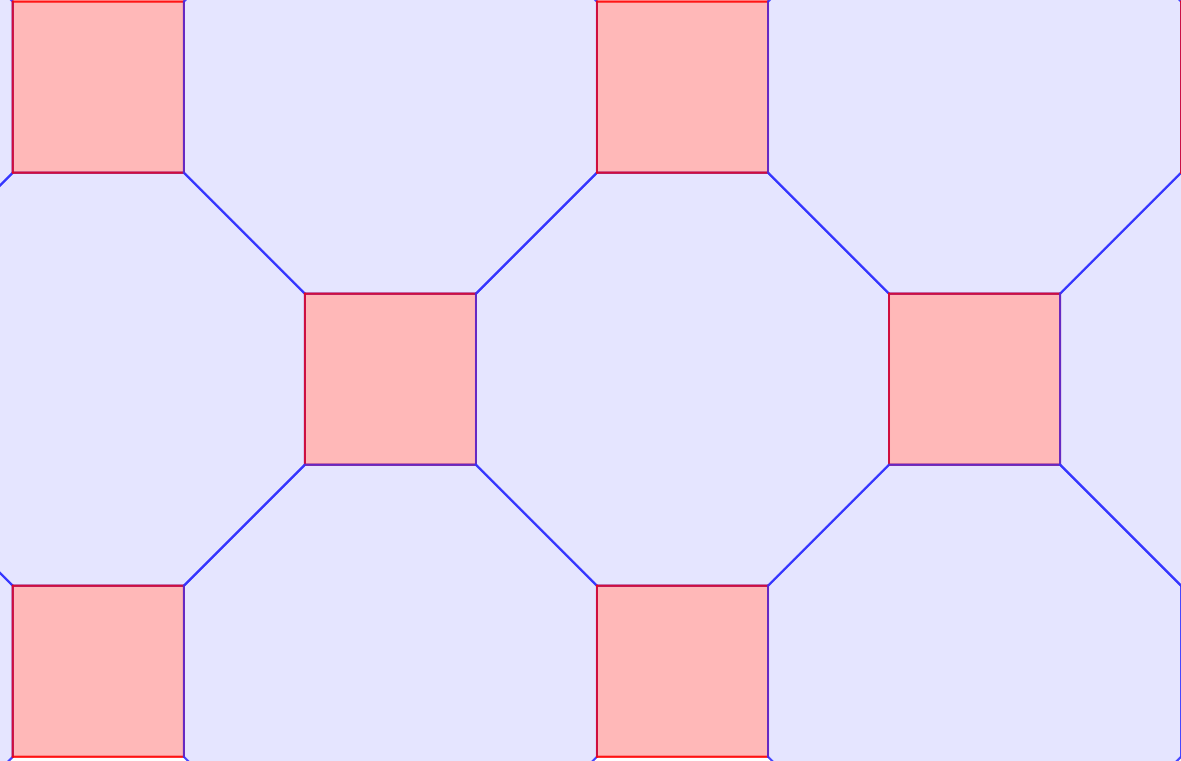
az n=4
esetet. Ekkor
amiből
azt kapjuk, hogy
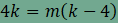 , ,
A 16-ot két egész szám szorzatára kell
bontanunk, ezt csak úgy tehetjük meg, hogy
Az utolsó szorzattá bontásból m=k=8, valamint a (4, 8, 8) síkkitöltés adódik. Az alábbi animáció mutatja, hogy ez is megvalósítható.
Végül
vizsgáljuk meg az n=6
esetet. Ekkor
illetve
adódik. A sokszögek oldalszámára tett
korábbi feltevésünk alapján
ami lehetetlen, így m=6 marad. Ekkor
viszont
k=6,
így a (6, 6, 6) síkkitöltést kapjuk, ami csak egyfajta sokszöget
használ
és már
korábban is megtaláltuk. |
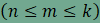
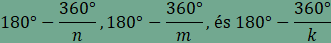 .
.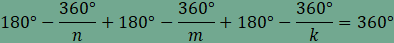 ,
,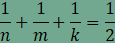 .
. ,
akkor az
,
akkor az 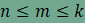
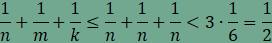 ,
,
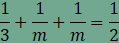 ,
,
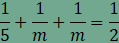 ,
,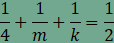
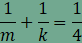 ,
,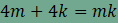 ,
,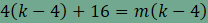 ,
,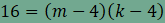
 . Az első
felbontásból
. Az első
felbontásból
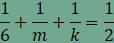 ,
,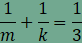
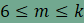 . Ha
. Ha 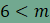
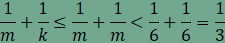 ,
,