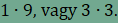| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
Keressük
meg a sík összes olyan síkkitöltését, amely a
következő feltételeknek eleget tesz!
|
|
Egy
korábbi feladatban megvizsgáltuk
azokat a
síkkitöltéseket, amelyek csak egyfajta szabályos sokszöget használnak.
Ilyenből
3 féle létezik: ezek szabályos háromszögekből, négyszögekből vagy
hatszögekből
építkeznek. Ha legalább kétfajta szabályos sokszöget használunk, akkor
egy
csúcsnál legalább 3, legfeljebb 5 szabályos sokszög érintkezhet.
Valóban,
hiszen a szabályos sokszögek közül a háromszögnek a legkisebb a belső
szöge
(60°), ebből pedig pontosan 6 darab kell egy hézagok és átfedések
nélküli lefedéshez,
ezért 6 sokszögnél több semmiképpen nem vehet részt a kitöltésben.
Pontosan 6
sokszög is csak akkor, amikor szabályos háromszögekből építkezünk. A
másik
oldalról viszont: a csomópontoknál két sokszög nyilván nem elegendő,
hiszen
minden szabályos sokszög konvex, ezért a szögei 180°-nál kisebbek, így
két
sokszög hézagmentesen nem tudja egyetlen csomópontnál sem kitölteni a
síkot.
Ebben a feladatban azokat a kitöltéseket keressük, amelyeknél minden
csomópontnál 4 sokszög találkozik. Az egy csomópontban 3 szabályos
sokszöget
tartalmazó síkkitöltéseket egy másik feladatban
tanulmányoztuk. Legyen
az egy csúcsnál találkozó sokszögek oldalainak száma n,
m
és k és l
A
csomópontoknál a kitöltés nem tartalmaz sem hézagot sem
átfedést, ezért
amiből összevonás, rendezés és egyszerűsítés után 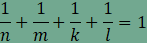 . .
Ha most
ami ellentmond a fenti egyenlőségnek.
Ebből adódóan n
értéke 3 vagy 4. Vizsgáljuk ezúttal az n=4 esetet, amikor
a legkevesebb oldalt tartalmazó sokszög négyzet. Ekkor
amiből rendezés után azt kapjuk, hogy
amiből Vizsgáljuk az n=3
esetet. Ekkor
Először nézzük meg, hogy mi a helyzet, ha
a csomópontban már nincs több háromszög, azaz ha Ebben az esetben
és így Visszahelyettesítés után
amiből
Most azt az esetet elemezzük, amikor n=3
és a csomópontok további szabályos háromszöget is tartalmaznak, azaz m=3. Ebben
az esetben
A 9-et kell tehát két pozitív egész szám
szorzatára bontanunk. Ezt megtehetjük úgy, hogy Az első esetben k=4 és l=12, a felbontás
pedig amit így kapunk a (3, 3, 4, 12), azaz minden csomópontban két
háromszög,
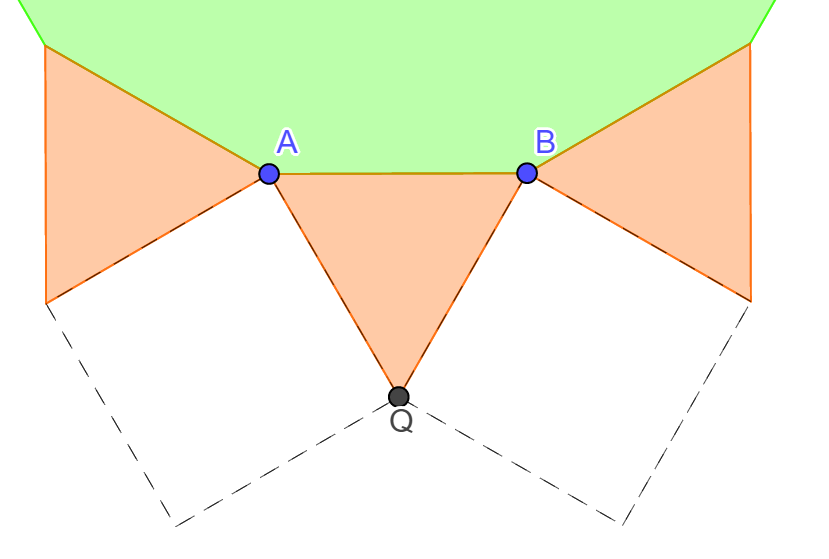
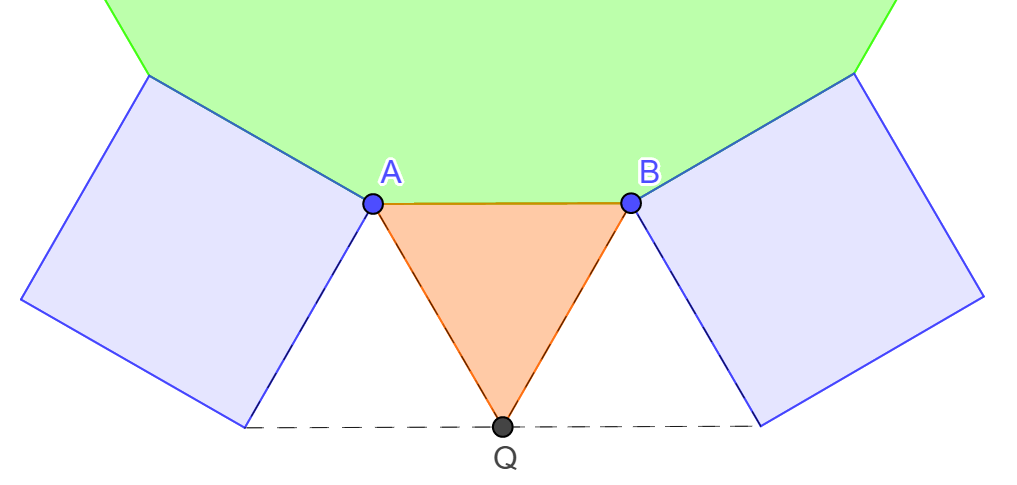
egy négyzet valamint egy 12-szög találkozik. Megmutatjuk, hogy ez a kitöltés nem
valósítható meg. Először is a 12-szögben nem lehet két szomszédos
oldal,
amelyek mindegyikéhez négyzet csatlakozik, mert akkor a két oldal közös
csúcsában a feltételekkel ellentétben 2 négyzet találkozna. Ezért a
12-szögben
van olyan oldal, amelyhez háromszög csatlakozik (az ábrákon AB jelöli). A
következő esetek lehetségesek.
Ha
pedig a 9-et úgy bontjuk szorzattá, hogy mindkét tényező 3,
akkor k=l=6 adódik, az
ennek megfelelő felbontás
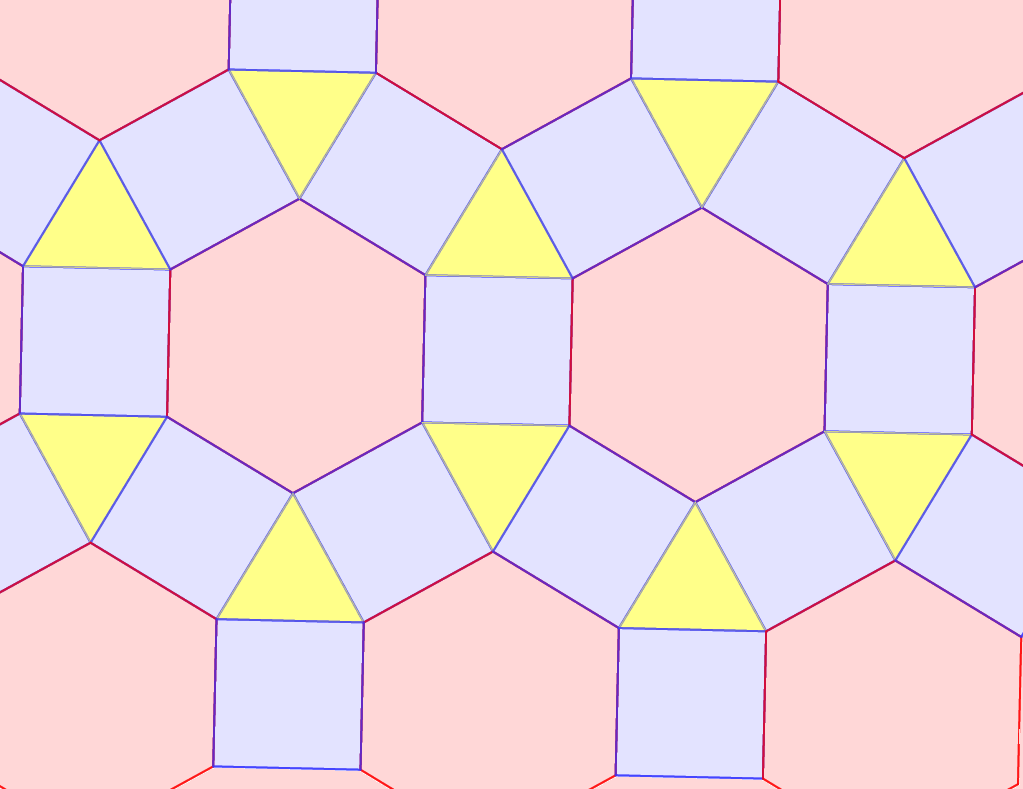
pedig a (3, 3, 6, 6), ami megvalósítható és az alábbi animáció
szemlélteti.
|
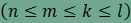
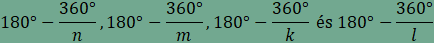 .
. ,
, ,
akkor az
,
akkor az 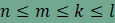
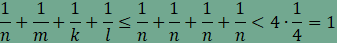 ,
,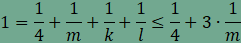 ,
,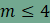 ,
majd
,
majd 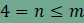
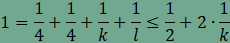
 ,
végül
,
végül 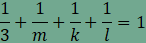 .
.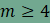
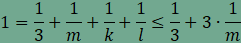 ,
,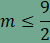 ,
, 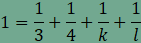 ,
,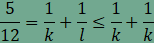 ,
,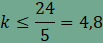 ,
, 
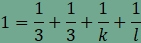 ,
,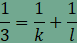 ,
,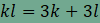 ,
,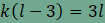 ,
,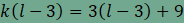 ,
,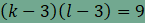 .
.