| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
Keressük meg a sík összes olyan síkkitöltését, amely a következő feltételeknek eleget tesz!
|
|
Egy korábbi feladatban megvizsgáltuk azokat a síkkitöltéseket, amelyek csak egyfajta szabályos sokszöget használnak. Azokat a síkkitöltéseket, amelyek 3 féle szabályos sokszöget használnak itt tanulmányoztuk. Itt pedig azokat vizsgáltuk, amelyek 4 féle sokszögből építkeznek. Ebben a feladatban azokat a kitöltéseket keressük, amelyekben minden csomópontnál 5 sokszög találkozik. Legyen
az egy csúcsnál találkozó sokszögek oldalainak száma n,
m
és k, l
és p
A
csomópontoknál a kitöltés nem tartalmaz sem hézagot sem
átfedést, ezért
amiből összevonás, rendezés és
egyszerűsítés után
Ha most
ami ellentmond a fenti egyenlőségnek.
Ebből adódóan n
értéke csak 3 lehet, azaz a feltételknek megfelelő síkkitöltés biztosan
tartalmaz szabályos háromszöget. Helyettesítsünk n helyére 3-at, így
Ha
ami nem lehetséges, ezért m=3. A kitöltés
tehát legalább két szabályos háromszöget tartalmaz. Visszahelyettesítés után azt kapjuk, hogy
Ha most
ami lehetetlen, ezért k=3. Eddigi
eredményeinket összefoglalva láthatjuk, hogy ha a kitöltésben 5 csúcs
találkozik a csomópontokban, akkor azok között legalább 3 szabályos
háromszög
van. Helyettesítsük vissza k=3-at,
így
Ha
l=3,
akkor p=6,
amiből a (3, 3,
3, 3, 6) síkkitöltést kapjuk, amelynek megvalósíthatóságát az alábbi
animációban láthatjuk.
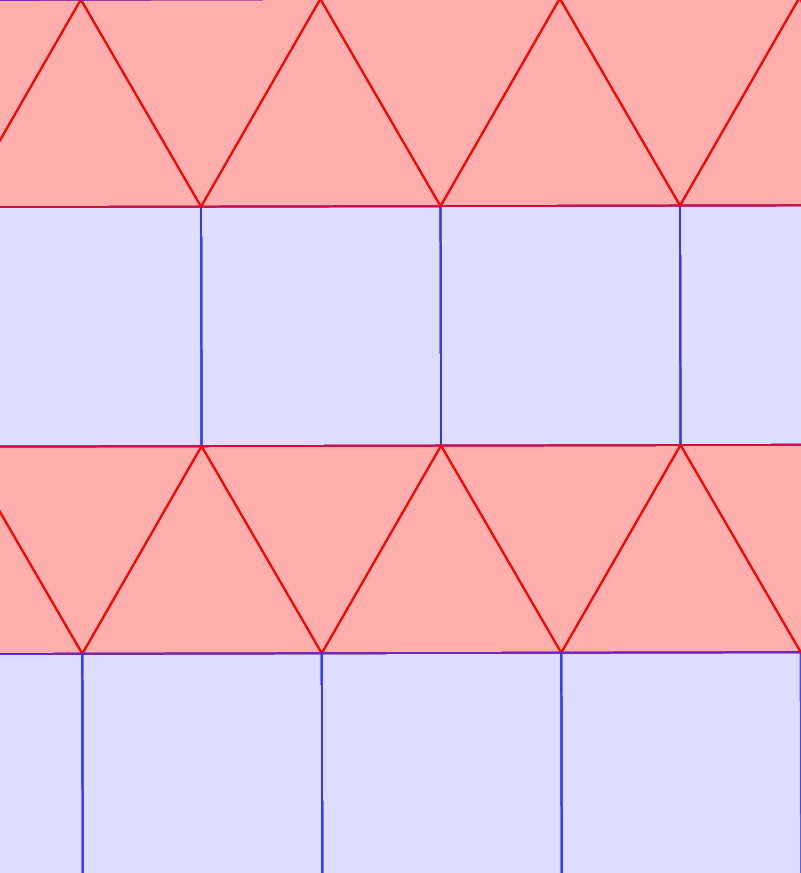
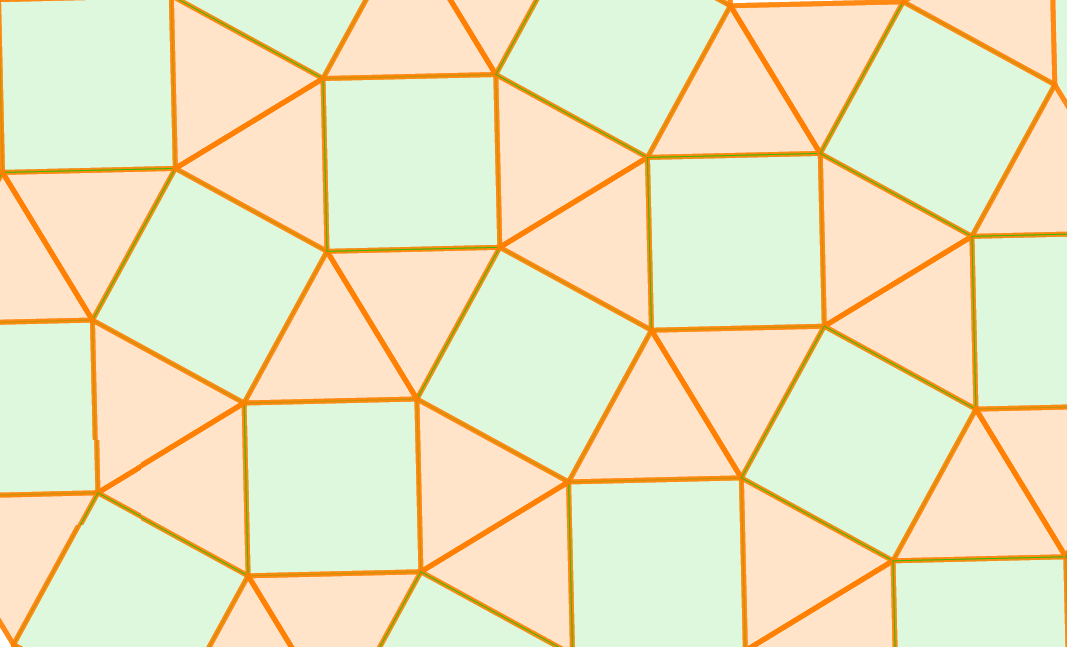
Ha l=4, akkor p=4, amiből a (3, 3, 3, 4, 4) síkkitöltést kapjuk, amely kétféleképp is megvalósítható. Ezeket az alábbi animációkban figyelhetjük meg.
Ha pedig
ami
ellentmondás, ezért több megoldása
nincs a feladatnak. |
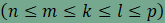
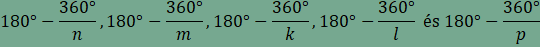 .
.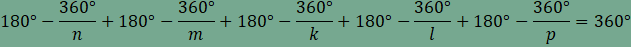 ,
,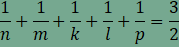 .
.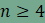 ,
akkor az
,
akkor az 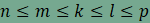
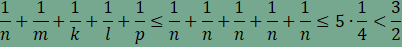 ,
,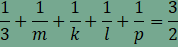
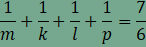
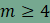
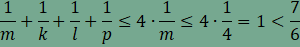 ,
,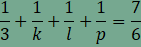
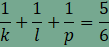 .
.
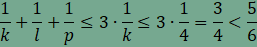 ,
,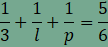 ,
,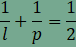 .
.
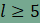 ,
akkor
,
akkor 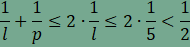 ,
,