| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
Ebben a feladatban a sík szabályos sokszögekkel való kitöltésével kapcsolatos eredményeinket foglaljuk össze. |
|
A sík
sokszögekkel való parkettázása (lefedése) alatt olyan
kitöltést értünk, amelyre a következő feltételek teljesülnek:
Szabályos
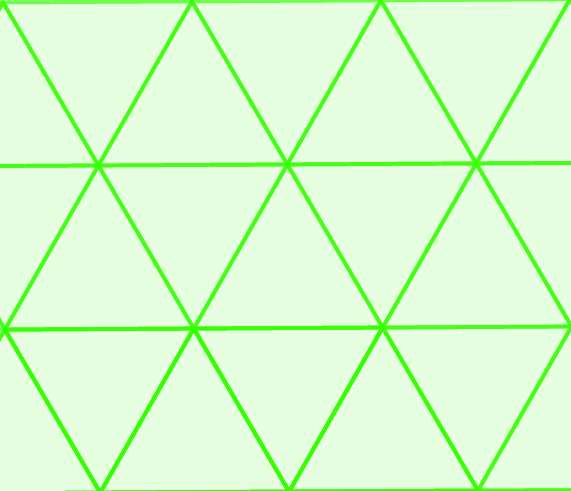
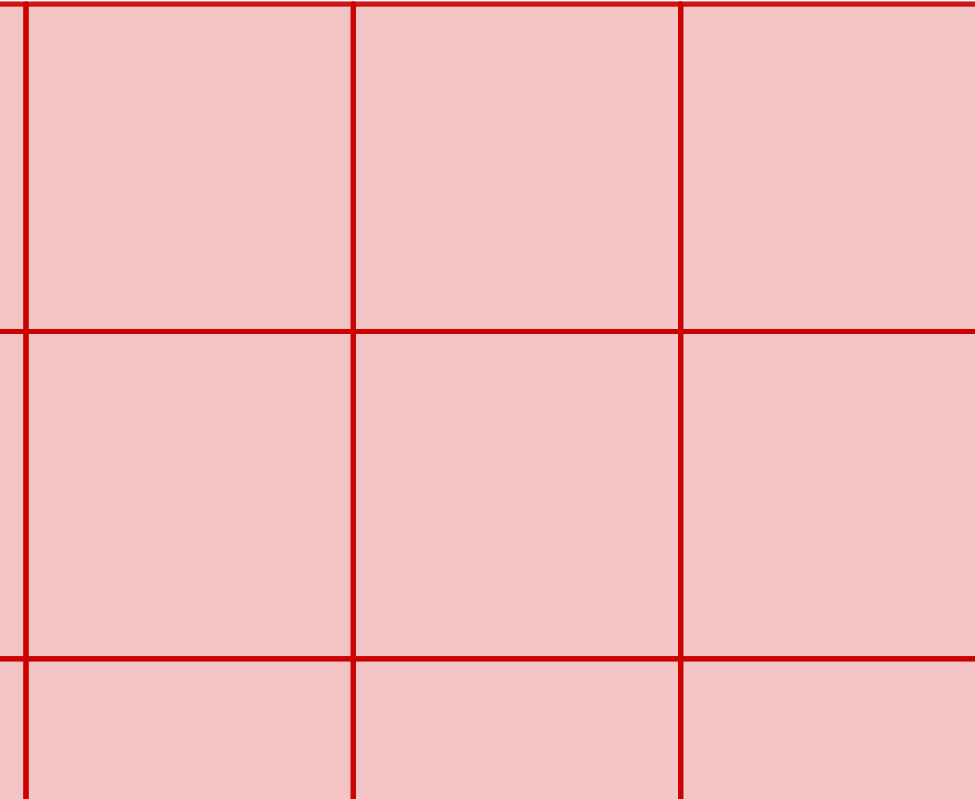
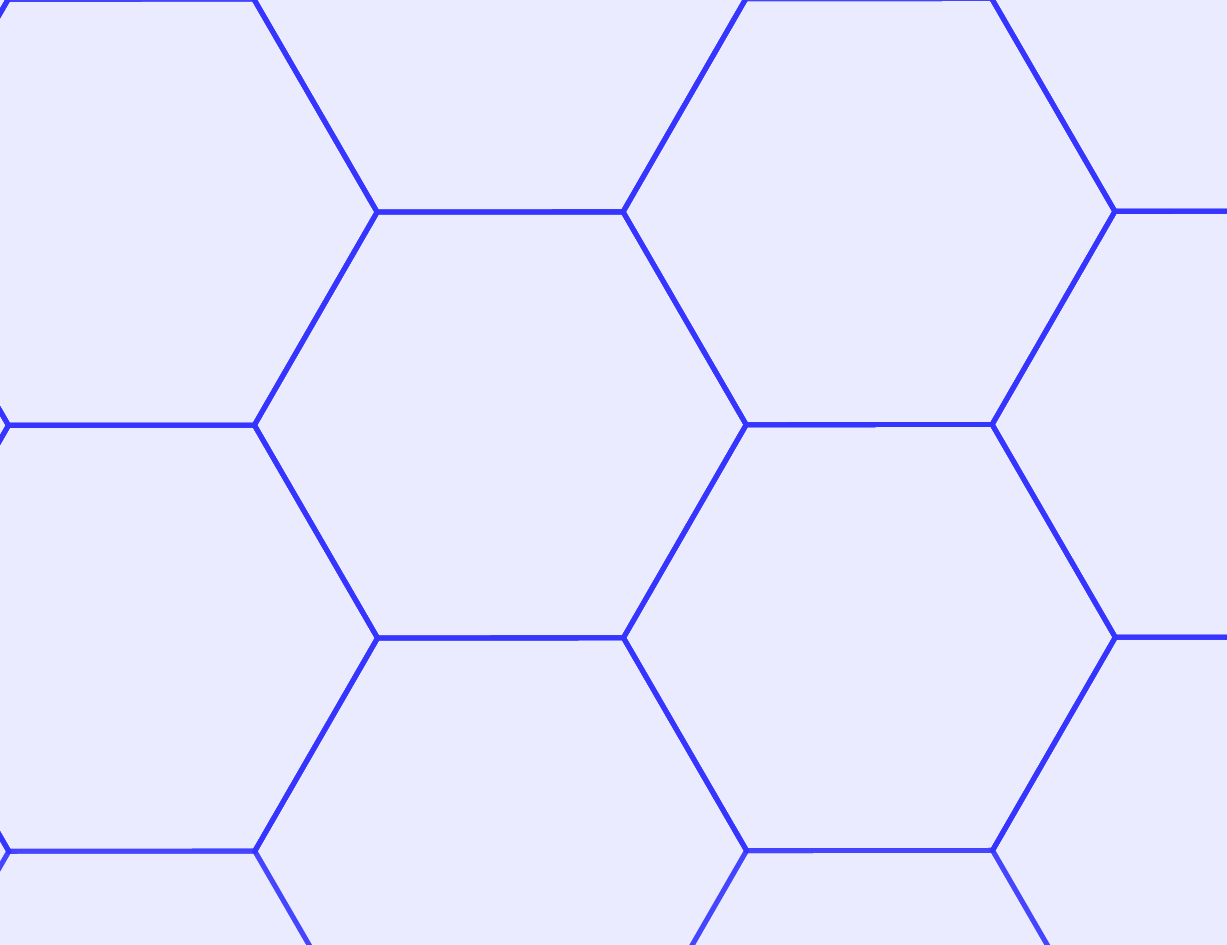
parketták A sík fenti feltételeknek megfelelő kitöltését szabályosnak nevezzük, ha a lefedésben résztvevő sokszögek egymással egybevágó szabályos sokszögek. Ezeket a kitöltéseket ebben a feladatban kerestük. Összesen 3 szabályos parketta létezik, ezek háromszögekből, négyzetekből vagy hatszögekből építkeznek.
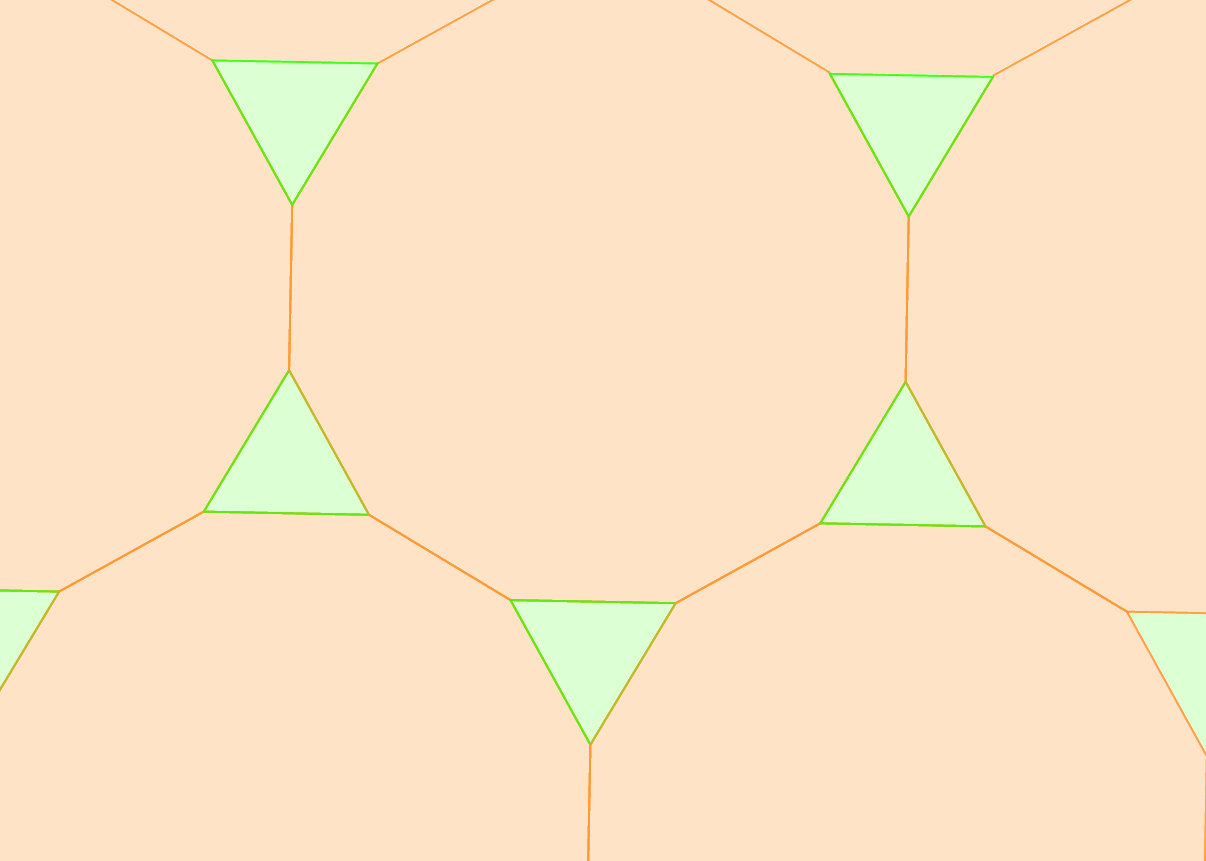
Félig szabályos
(Archimédeszi) parketták Ezek
olyan parketták, amelyek legalább kétféle szabályos sokszöget
használnak, és minden csomópontnál az ugyanolyan oldalszámú szabályos
sokszögekből mindig ugyanannyi van, és azok ugyanabban a sorrendben
követik
egymást. A félig szabályos parkettákat leírhatjuk a csomópontban
találkozó
sokszögek oldalainak számával: pl. a (4, 6, 12) jelölés olyan parkettát
takar,
amelyben minden csomópontnál egy szabályos négyszög, egy szabályos
hatszög
valamint egy szabályos 12-szög találkozik. Megmutattuk,
hogy egy ilyen parkettában minden csúcsnál 3, 4
vagy 5 sokszög találkozik. Összesen
3 olyan félig szabályos síkkitöltés létezik,
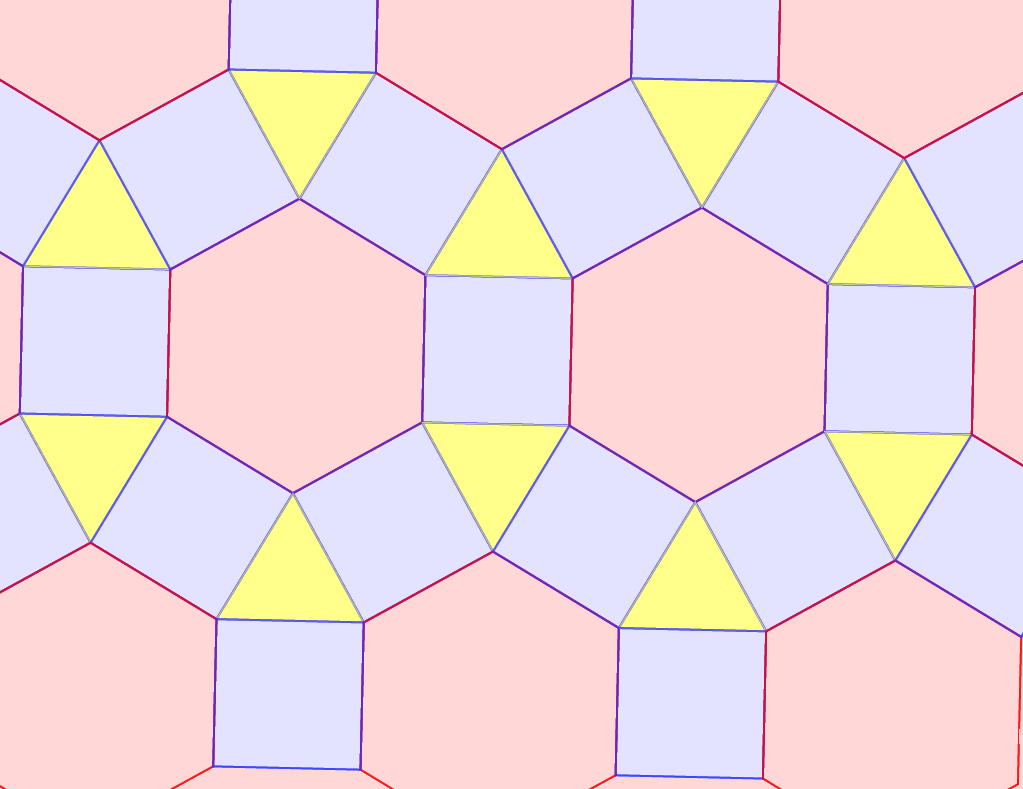
amelyben a csomópontoknál 3 sokszög találkozik; ezek rendre a (3, 12,
12), a
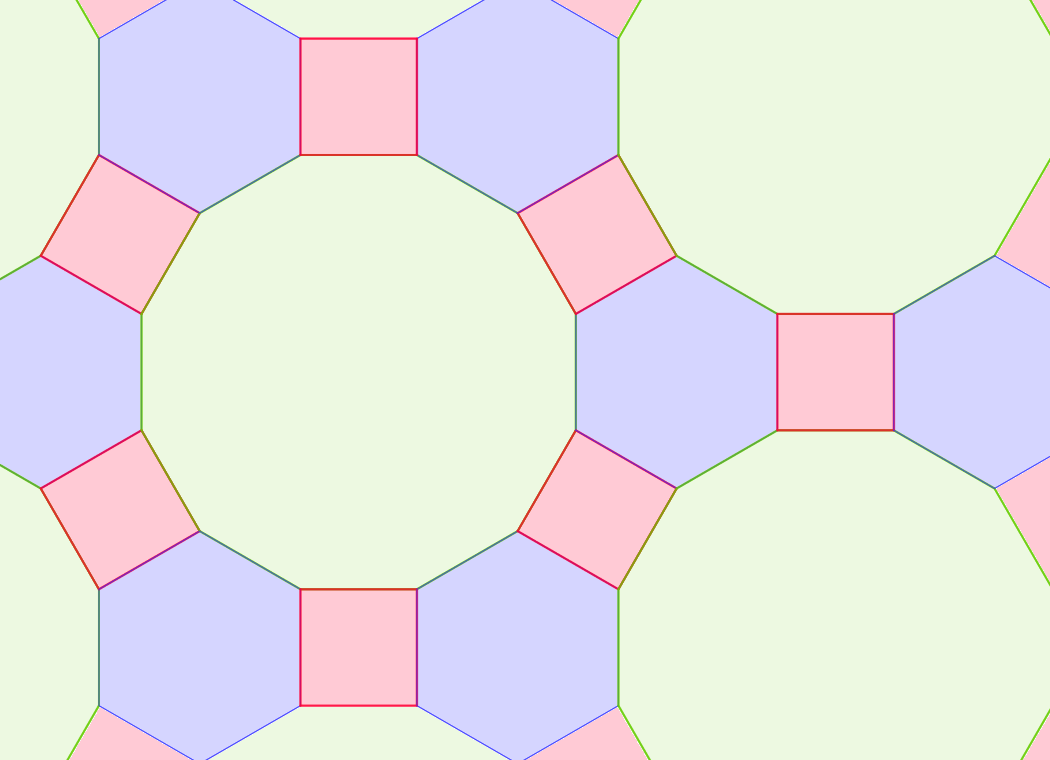
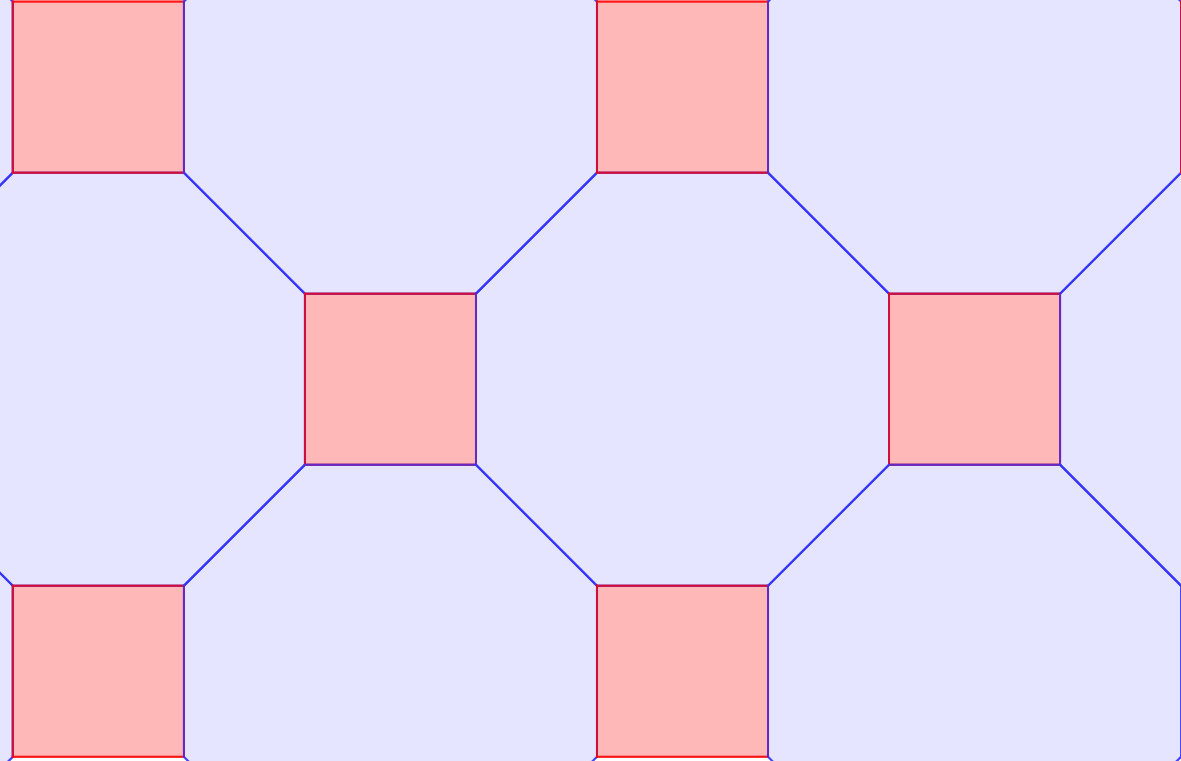
(4, 6, 12) illetve a (4, 8, 8) parketták. Ezeket
ebben a feladatban vizsgáltuk.
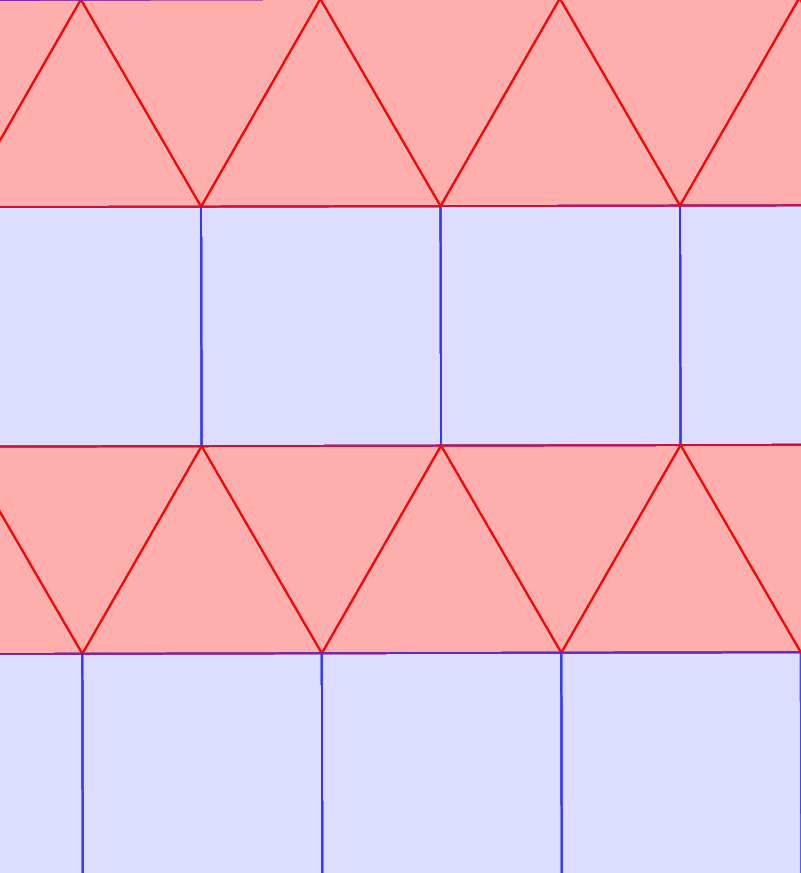
Összességében tehát 8 különböző félig szabályos síkkitöltés létezik. Azokat
a síkkitöltéseket, amelyek
homogénnek
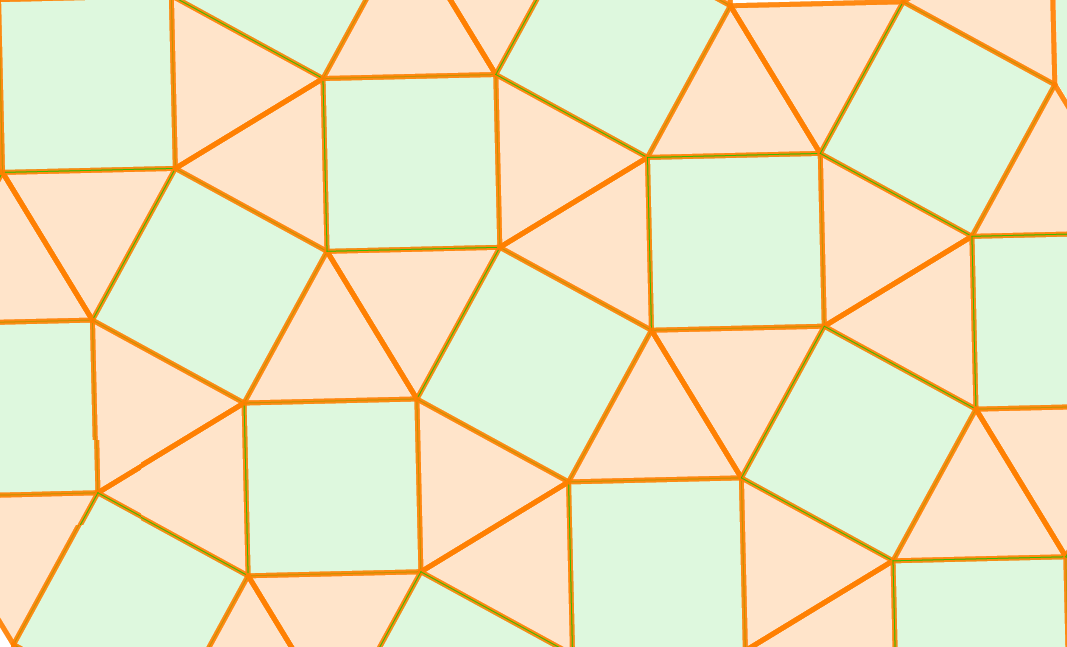
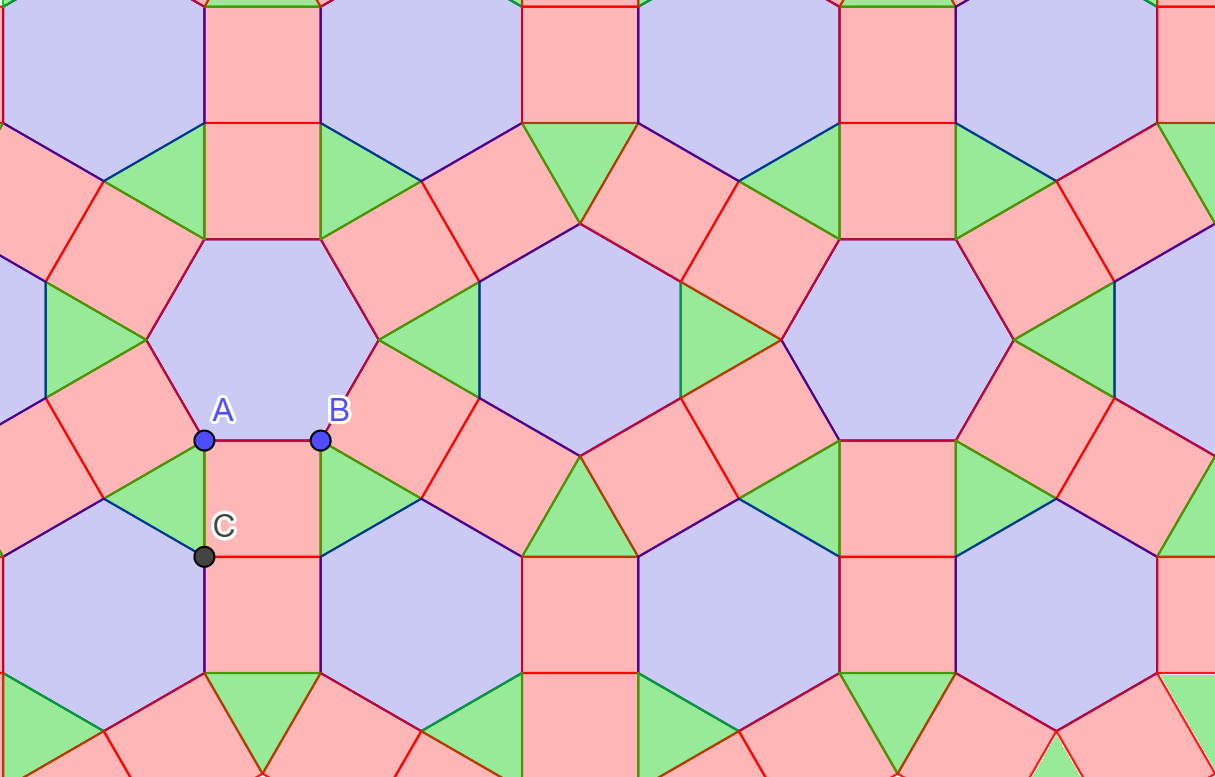
nevezzük. A szabályos és a félig szabályos parketták mind homogének, de rajtuk kívül további síkkitöltéseket is találunk. Az alábbi animáció egy ilyen homogén parkettát mutat be. A parketta (3, 4, 4, 6) típusú síkkitöltés. Az A és C csúcsoknál azonban a sokszögek nem ugyanabban a sorrendben követik egymást (C-nél a két négyzet oldal mentén, A-nál pedig csúcsok mentén érintkezik), ezért ez a síkkitöltés nem félig szabályos.
|