| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
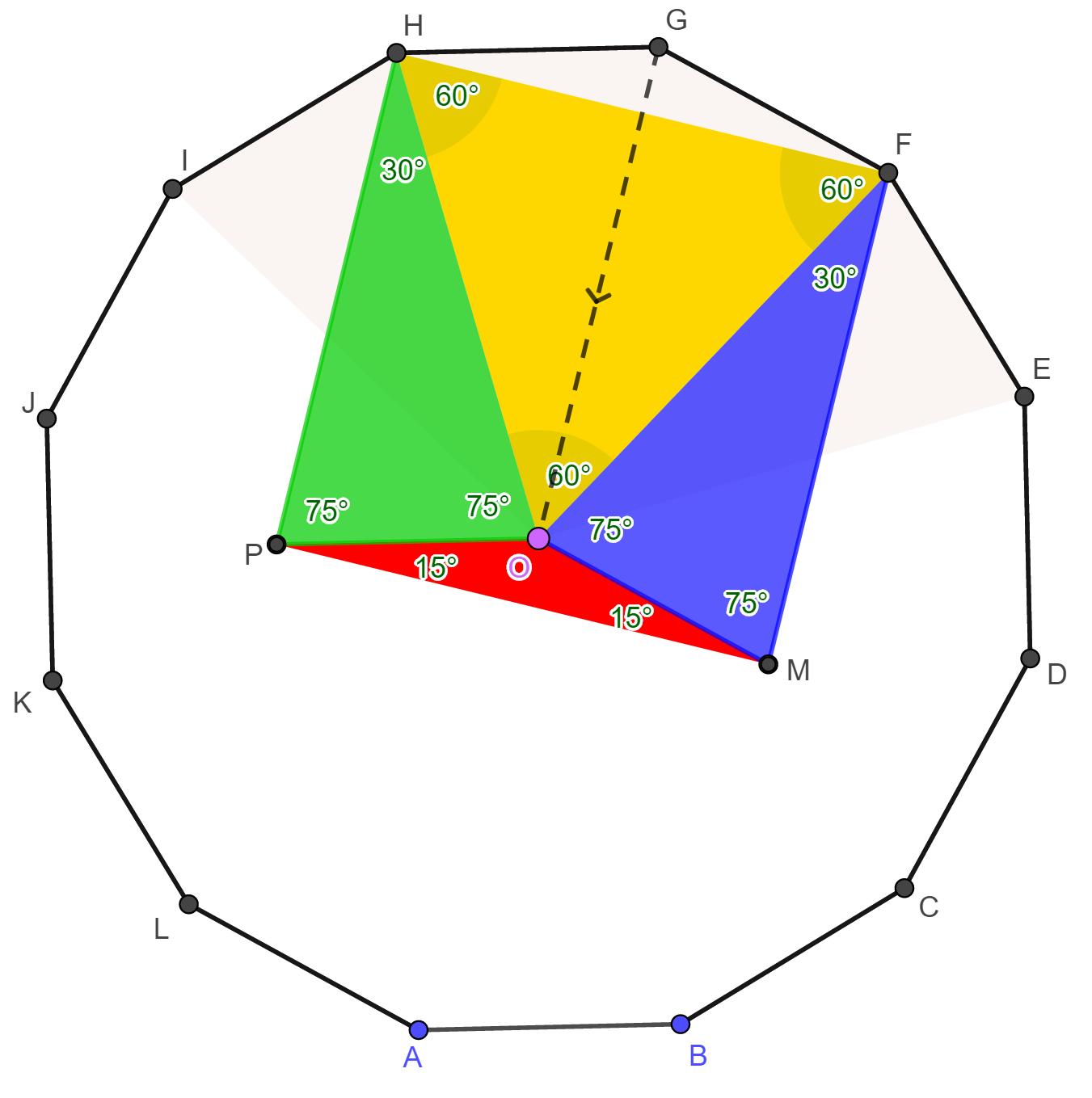
Mutassuk meg, hogy a szabályos tizenkétszög területe háromszorosa a sokszög köré írt kör sugarával megegyező oldalú négyzet területének! |
|
A
12-szög középpontját jelöljük O-val.
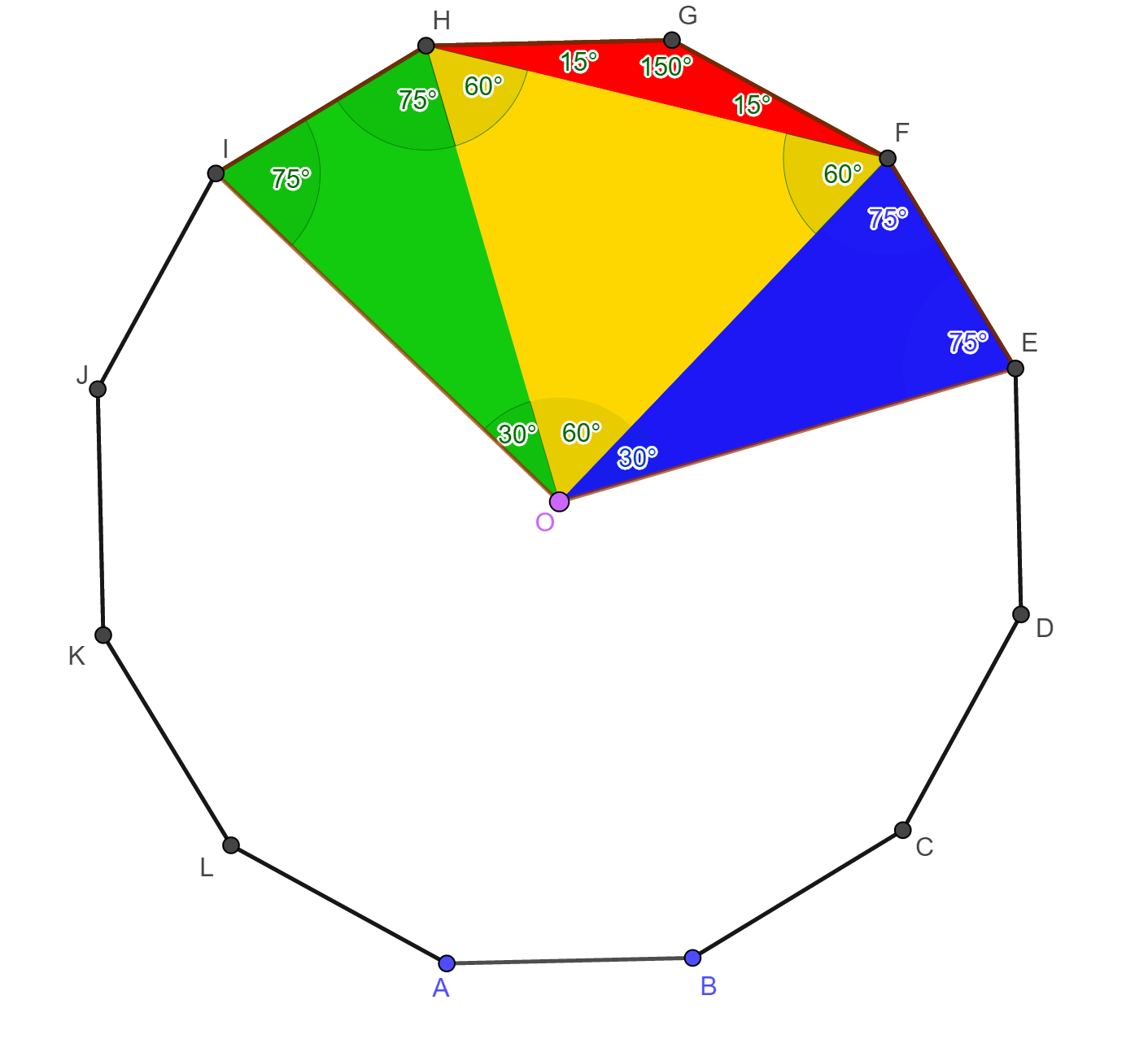
Megmutatjuk, hogy az
OEFGHI
hatszög (ld. ábra) átdarabolható egy olyan négyzetté, amelynek oldala
megegyezik a 12-szög köré írható kör sugarával. Ebből a feladat
állítása már
következik. Húzzuk
be az OF, OH és HF szakaszokat,
amivel az OEFGHI
hatszöget négy háromszögre bontjuk. Számoljuk ki a háromszögek szögeit! Mivel
a szabályos 12-szög egy belső szöge 150°, ezért a GHF
egyenlőszárú háromszögben
Az OEF
és a vele egybevágó OHI
háromszögekben az O
csúcsnál lévő szög
Most
forgassuk el az OEF
háromszöget az O
pont körül
-150°-kal, az OHI
háromszöget pedig 150°-kal. A forgatások után a két háromszög
képe rendre az OLA,
illetve az OAB
háromszögek. Mivel az L,
O,
F
pontok egy
egyenesre illeszkednek, továbbá LO=OF, ezért ha az OLA háromszög
csúcsait
eltoljuk az
Most
vizsgáljuk az OPM
háromszöget! Az előbbi észrevételünk
alapján
Ezzel
a feladat állítását beláttuk. |
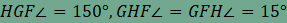 .
.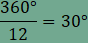
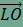
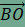 vektorral eltolt képe a
vektorral eltolt képe a 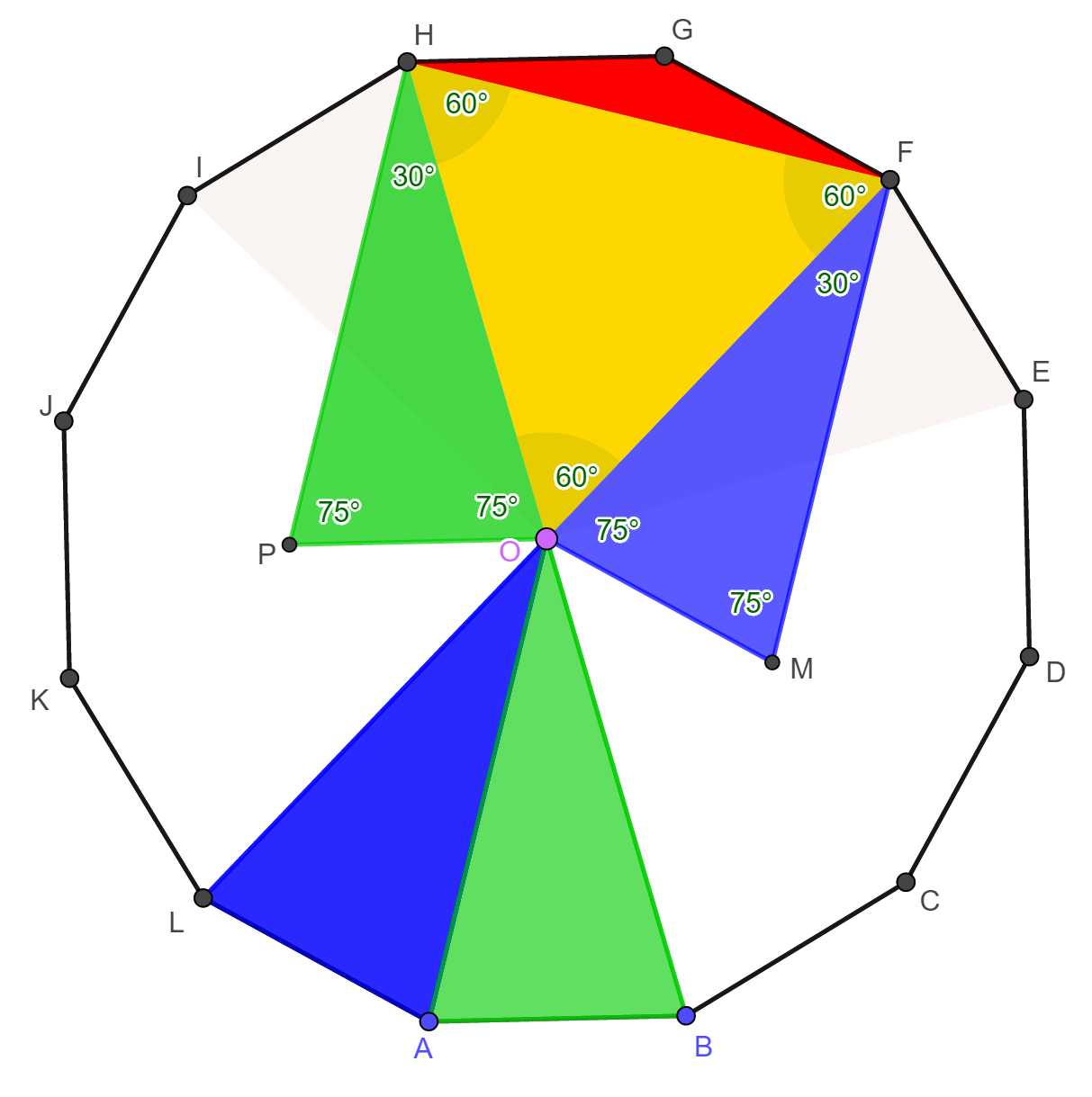
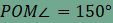 ,
,