| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
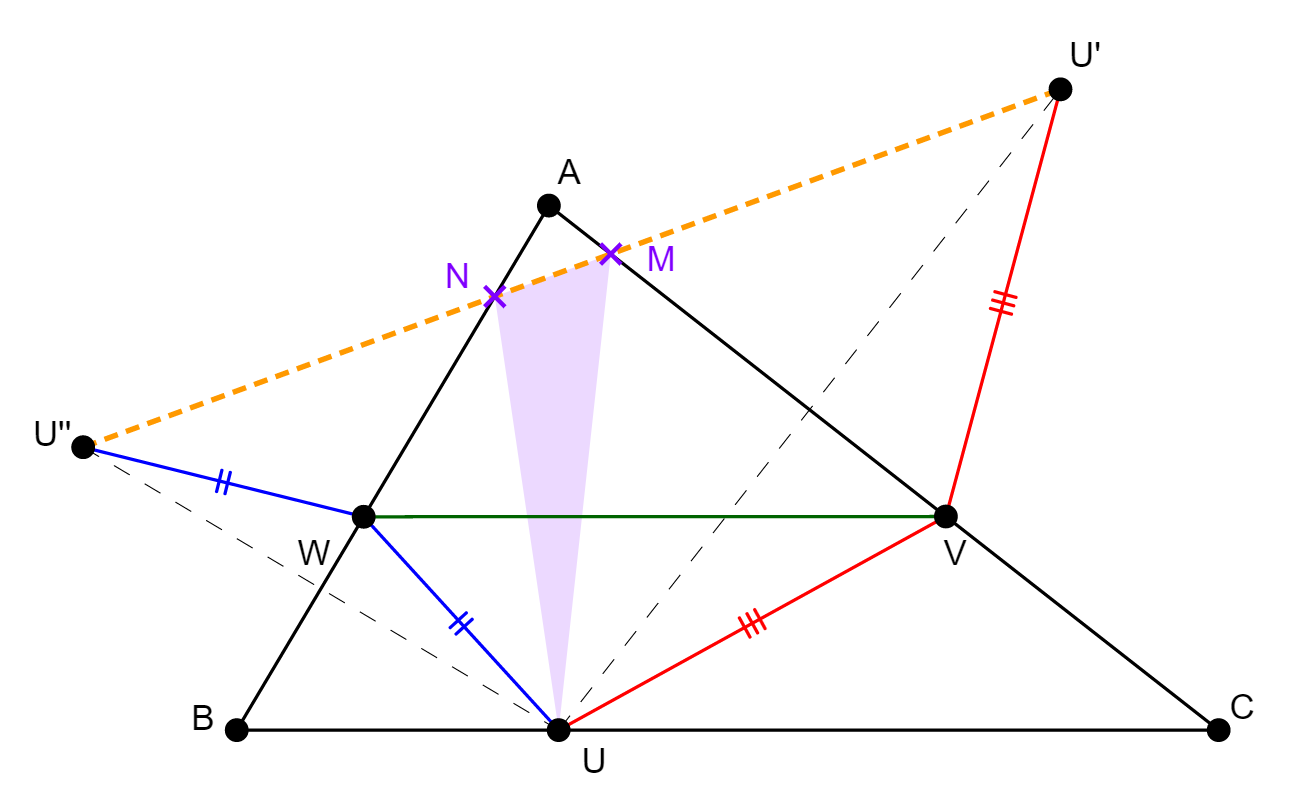
Markó Gábor, a Révai Miklós Gimnázium 10. osztályos tanulójának munkája Adott hegyesszögű háromszögbe írjuk be a legkisebb kerületű háromszöget! |
Fejér Lipót megoldása  Fejér Lipót (1880-1958) Tükrözzük az U
pontot AC és AB oldalegyenesekre, a tükörképek legyenek U’
és U”. A tengelyes tükrözés távolságtartó tulajdonsága miatt UV=U’V,
továbbá UW=U”W. Írjuk fel az UVW háromszög kerületét:
ez az összeg
pedig az előbbi megállapítások alapján egyenlő az
összeggel, ami pont az U’VWU” töröttvonal hossza. A V, W pontok mozgatása, de U pont rögzítése esetén U’ és U” pontok helyben maradnak, mert U és ABC háromszög meghatározza ezen két pontot. Rögzített U pont esetén az U’VWU” töröttvonal a szintén rögzített U’ és U” pontok között marad kifeszítve, hossza pedig mindig az UVW háromszög kerülete. Mivel két pont között mindig az egyenesvonalú összekötés a legrövidebb, ezért U’VWU” töröttvonal hossza és UVW háromszög kerülete akkor a legkisebb, ha U’, V, W és U” pontok egy egyenesre esnek. Tehát rögzített U pont esetén a legkisebb ilyen beírt kerületű háromszöget úgy kapjuk meg, hogy az U’U” szakasz kimetszi az AB és AC oldalakból az N és M pontokat (W, V pontok minimumhelyzete), és az így kapott UMN háromszög kerülete lesz minimális. Beláttuk, hogy ha az U pontot rögzítjük, akkor UMN háromszög kerülete lesz a minimális a beírt háromszögek közül, ezt megfigyelhetjük az animációban is. Meg kell még vizsgálnunk, hogy az U pont mozgatásával elérhető-e kisebb kerületű UMN háromszög ugyanezen módszerrel. Mivel
ezért UMN háromszög kerülete akkor minimális, ha U’U” is minimális. Vegyük észre, hogy 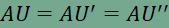 , ,a tükrözés távolságtartó tulajdonsága miatt, tehát AU’U” egyenlőszárú háromszög, amelyben U’U” szakasz a háromszög alapja. A tükrözés szögtartó tulajdonsága alapján pedig tudjuk, hogy
és 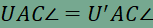 . .Ezen
megállapítások alapján
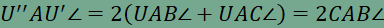 , ,ezért A célunk, hogy az AU’U” háromszögben az U’U” alap a lehető legkisebb legyen úgy, hogy minden AU’U” háromszög csúcsnál levő szöge megegyezik. Ezen egyenlőszárú háromszögek közül annak a legkisebb az alapja, amelynek a szára is a legrövidebb. Az AU’U” háromszög szárai azonban AU szakasz hosszának felelnek meg, tehát U’U” szakasz hossza akkor minimális, ha AU hossza is minimális. Az AU szakasz A pont összeköttetése a BC szakasz egy pontjával. Egy pont és egy egyenes legrövidebb összekötése azonban a pontból az egyenesre állított merőleges szakasz hossza. Ebből következik, hogy az AU szakasznak BC-re merőlegesnek kell lennie, azaz AU az ABC háromszög A csúcsához tartozó magassága. Innen pedig már megszerkeszthetjük a legkisebb kerületű beírt háromszöget a következő módszerrel. Legyen az A-ból induló magasság talppontja E, az E pont AC és AB oldalakra vonatkozó tengelyes tükörképe pedig E’ és E”. Az E’E” szakasz kimetszi AC és AB oldalakból a minimális kerületű beírt háromszög másik két csúcsát, F-et és G-t, ezen minimális kerület nagysága pedig az E’E” szakasz hosszával egyezik meg. Minden EFG háromszögtől eltérő UVW beírt háromszög kerülete nagyobb, mert ha U pontja nem esik egybe E-vel, ekkor E’E”<U’U”, azaz
Ha pedig V és W közül valamelyik nem esik egybe F-fel vagy G-vel, ekkor pedig az E’FGE” töröttvonal biztosan rövidebb, mint az E’VWE” törött vonal hossza, így
minden esetben teljesül. A megoldásunk során E pontot az
A csúcshoz tartozó magasság talppontjaként, F és G
pontokat pedig az E pont megfelelő tükörképei segítségével határoztuk
meg. Az ABC háromszögben viszont minden A csúcsra vonatkozó
eljárást elvégezhettünk volna akár a B ponton is, azaz U pont
tükrözése helyett V pontot tükrözhettük volna az AB és BC
oldalakra, és így haladhattunk volna tovább. Ebben az esetben a B-ből
kiinduló magasság talppontja F lenne, és F tükrözésével majd E
és G pontok kimetszésével kaptuk volna meg a minimális kerületű
háromszöget. Azt már beláttuk, hogy pontosan egy legkisebb kerületű háromszög
van, ezért az A-ból és B-ból kiinduló konstrukció során kapott két
háromszög megegyezik. A C pontból való kiindulás esetén is erre a
következtetésre jutnánk, amelyből következik, hogy az E, FG
pontok a háromszög egy-egy magasságának talppontja. Tehát bebizonyítottuk a
talpponti háromszög minimum tulajdonságára vonatkozó alábbi tételt, és a
feladatot is megoldottuk. Adott hegyesszögű háromszögbe írt háromszögek közül a talpponti háromszög kerülete a legkisebb.
|
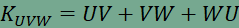
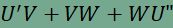
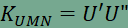
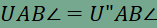
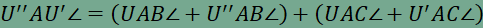 ,
,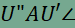 nagysága független
nagysága független 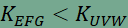 .
.