Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
| Adott konvex
négyszögben van-e olyan pont, amelynek a négyszög csúcsaitól vett
távolságösszege minimális? |
|
Ennek
a
feladatnak a bizonyításához elég felhasználnunk a
háromszög-egyenlőtlenséget.
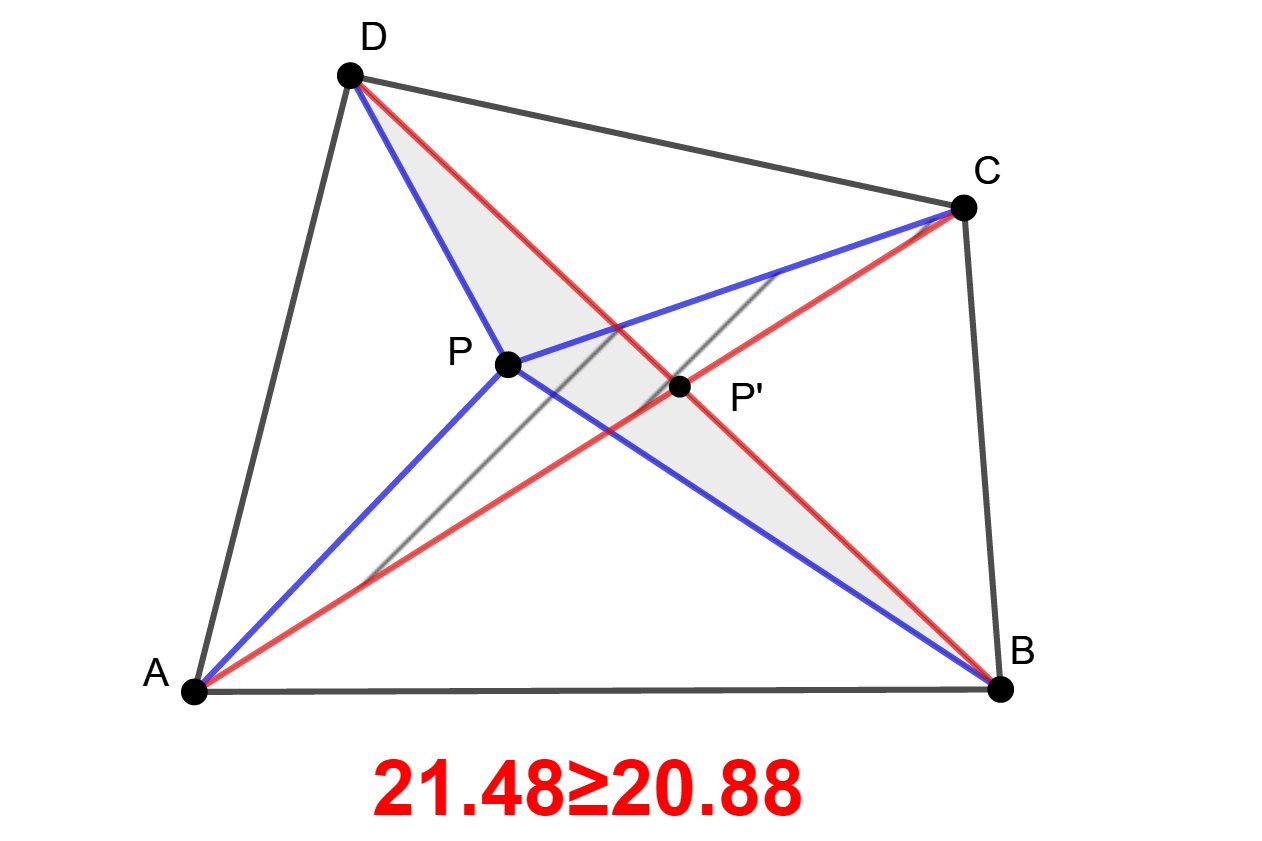
Ahogyan azt az animáció is mutatja, a csúcsoktól vett
távolságösszeg a PA+PB+PC+PD
összegnek felel meg. Húzzuk be a négyszög átlóit, legyen
az átlók
metszéspontja
P’. A háromszög-egyenlőtlenség teljesül
az APC
háromszögben
és a BPD
háromszögben, ez
alapján
AC=P’A+P’C≤PA+PC,
és BD=P’B+P’D<PB+PD.
Azaz a kérdéses összeget alulról becsülve PA+PC+PB+PD≥P’A
+ P’C
+ P’B + P’D.
Egyenlőség
akkor
és csak akkor lehetséges, ha a P
és P’ pontok egyebesnek, ekkor a PA+PB+PC+PD
összeg
minimális értéke az átlók összege, azaz AC+BD
=P’A+P’C+P’B+P’D,
ahol
P’ az átlók metszéspontja.
|