|
Menü
|
Ha
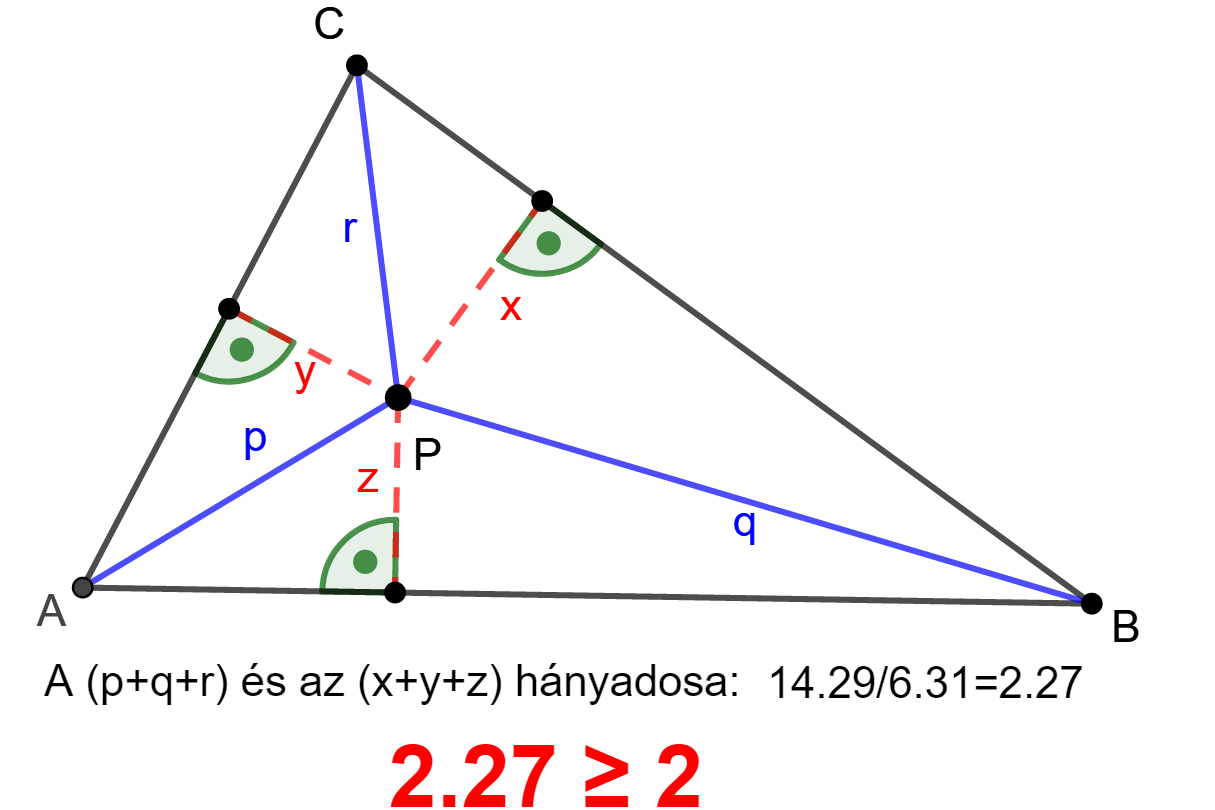
az ABC
háromszög belsejében levő P
pont távolsága a csúcsoktól p, q,
r, az oldalaktól x,
y, z, akkor keressük
meg a
tört
minimális értékét!
|
Az animáció alapján
megfogalmazható sejtés szerint
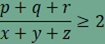 .
A
sejtés Erdős Páltól(1913-1996) származik, az első megoldást
L. J. Mordell(1888-1972) adta.
 |  | | Erdős Pál | L. J. Mordell |
Tegyük fel, hogy p,
q,
r
rendre a P
pontnak az A,
B,
C
csúcsoktól, x,
y,
z
pedig a BC,
CA,
AB
oldalaktól mért távolsága, ahogyan azt az ábra mutatja.
Bebizonyítjuk az alábbi segédtételt:
A
bizonyításhoz tükrözzük a B és C
csúcsot
a BAC szög szögfelezőjére, a tükörképek C', illetve
B', a P pont helyben marad. Ahogyan azt a szerkesztés is mutatja, az
AB'C' háromszög oldalai most a tükrözés távolságtartása miatt AC'=b,
B'C'=a és B'A=c, továbbá a P pont távolsága B'C', C'A, AB' oldalaktól
rendre x', z, y.
Legyen az AB'C' háromszög A-hoz tartozó magssága 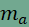 . .
Ez a szakasz biztosan nem hosszabb, mint az A csúcstól a P ponton
át a B'C' egyenesig vezető bármely "út", azaz
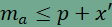 .
egyenlőtlenséget kapjuk, ahol a bal oldalon álló kifejezés pontosan az
AB'C' háromszög területének kétszerese. Az AB'C' háromszög területét
azonban felírhatjuk az APC', C'PB', B'PA háromszögek területének
összegeként is, így az
egyenlőtlenséget, majd ax' levonása után a bizonyítandó
összefüggést
kapjuk. Hasonló módon igazolható a másik két egyenlőtlenség is.
A segédtétel egyenlőtlenségeit átrendezve juthatunk el a
összefüggésekhez.
A kapott három egyenlőtlenség összeadása pontosan az Erdős-Mordell
egyenlőtlenséghez vezet, ugyanis
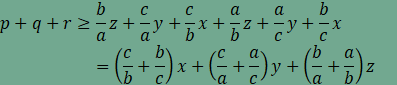
és
mivel egy pozitív számnak és reciprokának összege legalább 2, ezért
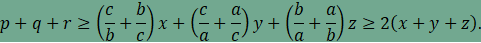
 ,
Az egyenlőség egyik feltétele, hogy
az oldalak és a reciprokaik összege pontosan 2 legyen, ez pedig csak
a=b=c esetén teljesül, azaz ha a háromszög szabályos. Szabályos
háromszög esetén azonban a leveztésben szereplő ABC és AB'C'
háromszögek egybeesnek, így az AP és az x' szakasz helyzete azonos az
AP és az x szakasz helyzetével. Továbbá 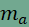 akkor és csak akkor
lehet egyenlő a p+x összeggel, ha P pont rajta van az akkor és csak akkor
lehet egyenlő a p+x összeggel, ha P pont rajta van az 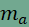 szakaszon,
és ugyanígy a P pontnak rajta kell lennie az szakaszon,
és ugyanígy a P pontnak rajta kell lennie az 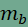 és és 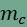 szakaszokon is,
azaz a B és C pontokhoz tartozó magasságokon is. Ebből következik, hogy
egyenlőség esetén a P pont csakis a szabályos háromszög magasságpontja
lehet. szakaszokon is,
azaz a B és C pontokhoz tartozó magasságokon is. Ebből következik, hogy
egyenlőség esetén a P pont csakis a szabályos háromszög magasságpontja
lehet.
|
|
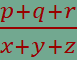
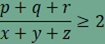 .
.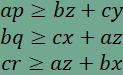
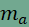 .
.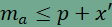 .
.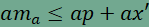
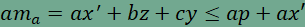
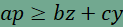
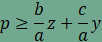 ,
,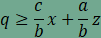 ,
,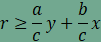
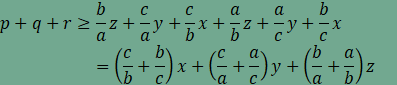
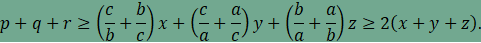
 ,
,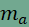 akkor és csak akkor
lehet egyenlő a p+x összeggel, ha P pont rajta van az
akkor és csak akkor
lehet egyenlő a p+x összeggel, ha P pont rajta van az 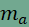 szakaszon,
és ugyanígy a P pontnak rajta kell lennie az
szakaszon,
és ugyanígy a P pontnak rajta kell lennie az 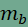 és
és 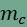 szakaszokon is,
azaz a B és C pontokhoz tartozó magasságokon is. Ebből következik, hogy
egyenlőség esetén a P pont csakis a szabályos háromszög magasságpontja
lehet.
szakaszokon is,
azaz a B és C pontokhoz tartozó magasságokon is. Ebből következik, hogy
egyenlőség esetén a P pont csakis a szabályos háromszög magasságpontja
lehet.