Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
Adott
az ABC
hegyesszögű háromszög, valamint egy 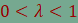 valós szám.
Vegyünk fel a háromszög AC
oldalán egy változtatható D
pontot, majd szerkesszünk olyan DEFG
téglalapot, amelynek EF
oldala a háromszög AB
oldalára illeszkedik, továbbá valós szám.
Vegyünk fel a háromszög AC
oldalán egy változtatható D
pontot, majd szerkesszünk olyan DEFG
téglalapot, amelynek EF
oldala a háromszög AB
oldalára illeszkedik, továbbá 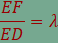 teljesül. teljesül.Milyen alakzaton mozog a téglalap G csúcsa, ha D befutja a háromszög AC oldalát? Észrevételeink alapján hogyan szerkeszthető (euklideszi értelemben) olyan DEFG négyzet, amelynek EF oldala az AB oldalra, D csúcsa az AC, míg G csúcsa a háromszög BC oldalára illeszkedik? |
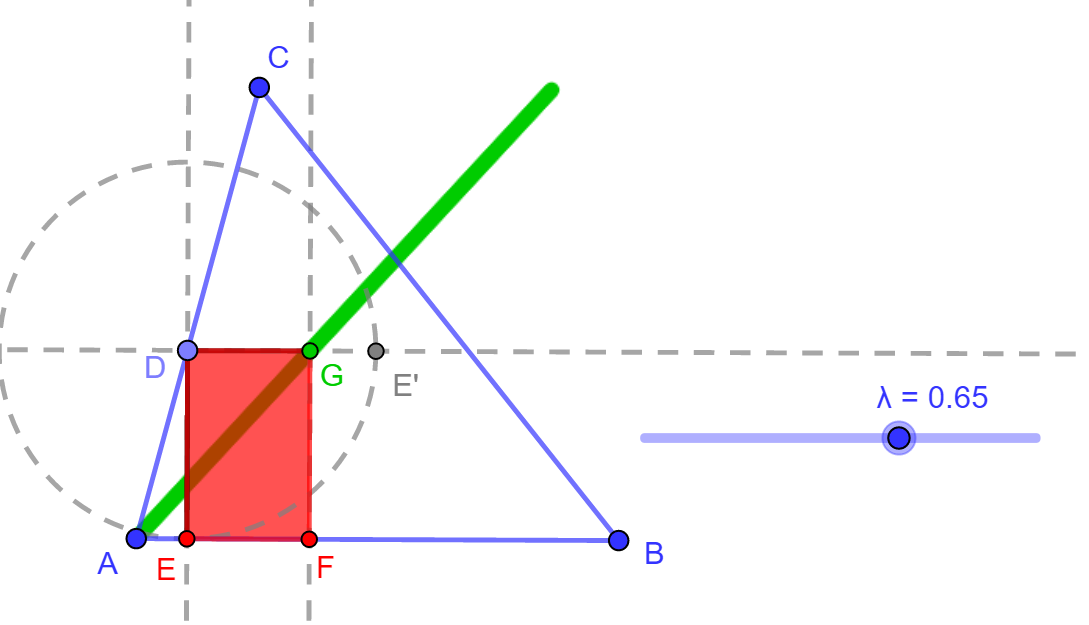
| A szerkesztés lépései 1. lépés: A D csúcsot az AC oldal pontjaként kell megszerkeszteni (Alakzat pontja funkció). 2. lépés: D-ből merőlegest állítunk az AB oldalra, így kapjuk az E pontot. 3. lépés: A D középpontú DE sugarú kör kimetszti a D ponton át DE-re emelt merőlegesből az E' pontot, nyilván DE=DE'. 4. lépés: A Centrális nyújtás funkció segítségével megszerkesztjük a G pontot; az E' pontot nyújtjuk a D középpontból, a hasonlóság aránya pedig 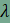 . .5. lépés: A G pontból merőlegest állítunk az AB egyenesre, a talppontként kapott metszéspont a téglalap G csúcsa. A G pont nyomvonalának megjelenítéséhez el kell indítani a D pontra vonatkozó animációt, a mértani hely mutatásához pedig aktiválni kell a Nyomvonal mutatása funkciót. A G pont egy A csúcsból kiinduló szakaszon mozog, ami azonnal következik abból, hogy a DEFG téglalapok mind középpontosan hasonlók egymáshoz, a hasonlóság középpontja az A csúcs, továbbá a hasonlóság során a középpont, a pont és képe egy egyenesre illeszkednek.
A háromszögbe írt négyzet szerkesztése már könnyen megtörténhet: a 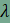 csúszka
értékét 1-re kell állítani, a D
csúcsot pedig
addig kell mozgatni az AC
oldalon, amíg a G
pont nem illeszkedik a BC
szakaszra. Ez persze euklideszi értelemben nem tekinthető
szerkesztésnek, de a fenti észrevételek segíthetnek ezen a problémán
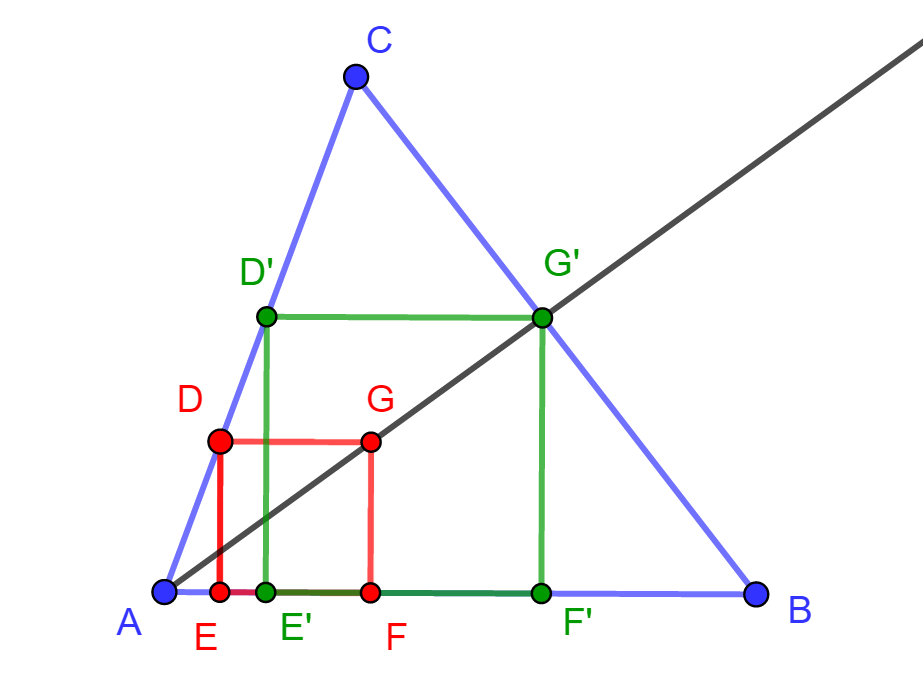
is. Elegendő ugyanis egyetlen olyan négyzetet szerkeszteni, amelynek D csúcsa az AC oldalra, EF oldala pedig az AB oldalra esik.
Az összes ilyen négyzet G
csúcsa egy szakaszt ír le, amelynek egyik végpontja A, így a szakaszt
tartalmazó félegyenes már megszerkeszthető. Ahol a félegyenes elmetszi
a BC
oldalt, ott lesz a szerkesztendő négyzet egyik csúcs. A
négyzet szerkesztése innen már teljesen nyilvánvaló. csúszka
értékét 1-re kell állítani, a D
csúcsot pedig
addig kell mozgatni az AC
oldalon, amíg a G
pont nem illeszkedik a BC
szakaszra. Ez persze euklideszi értelemben nem tekinthető
szerkesztésnek, de a fenti észrevételek segíthetnek ezen a problémán
is. Elegendő ugyanis egyetlen olyan négyzetet szerkeszteni, amelynek D csúcsa az AC oldalra, EF oldala pedig az AB oldalra esik.
Az összes ilyen négyzet G
csúcsa egy szakaszt ír le, amelynek egyik végpontja A, így a szakaszt
tartalmazó félegyenes már megszerkeszthető. Ahol a félegyenes elmetszi
a BC
oldalt, ott lesz a szerkesztendő négyzet egyik csúcs. A
négyzet szerkesztése innen már teljesen nyilvánvaló.
|