Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
Adott
az O
középpontú kör, valamint az 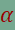 és és 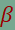 hegyesszögek.
Szerkesszünk háromszöget, amelynek két szöge hegyesszögek.
Szerkesszünk háromszöget, amelynek két szöge 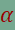 és és 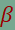 , az adott kör
pedig a körülírt köre! , az adott kör
pedig a körülírt köre! |
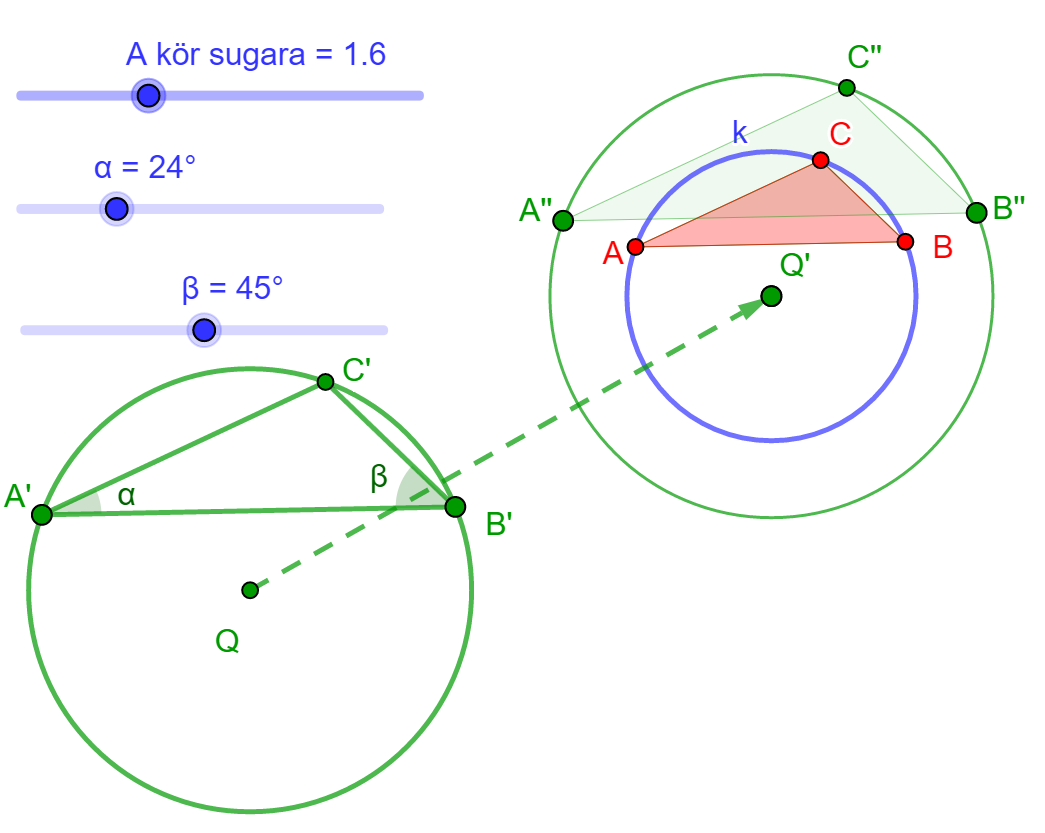
| A szerkesztés lépései 1. lépés: Tetszőleges A'B' alapra megszerkesztjük az A'B'C' háromszöget, amelynek A'-nél lévő szöge 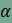 , B'-nél lévő szöge , B'-nél lévő szöge 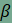 . .2. lépés: Megszerkesztjük az A'B'C' háromszög köré írt kör Q középpontját, valamint körülírt körét. 3. lépés: A Q pontot, valamint az A'B'C' háromszöget eltoljuk úgy, hogy a Q pont képe az adott kör O középpontjába kerüljön. Az A'B'C' háromszög képe A''B''C''. 4. lépés: Az A''B''C'' háromszög középpontosan hasonló a szerkesztendő háromszöghöz, hasonlóságuk középpontja az O pont, hasonlóságuk aránya pedig a körülírt köreik sugáranak hányadosa. Ezért a Centrális nyújtás funkció segítségével megszerkesztjük az A''B''C'' háromszöghöz hasonló ABC háromszöget úgy, hogy ABC körülírt köre az adott kör legyen. Az alábbi szerkesztésben az eltolást és a középpontos hasonlóságot is csúszka (animáció) segítségével valósítottuk meg.
A feladatnak a bemenő adatok tetszőleges megválasztása mellet egybevágóságtól eltekintve mindig egyértelmű megoldása van. |