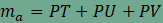Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
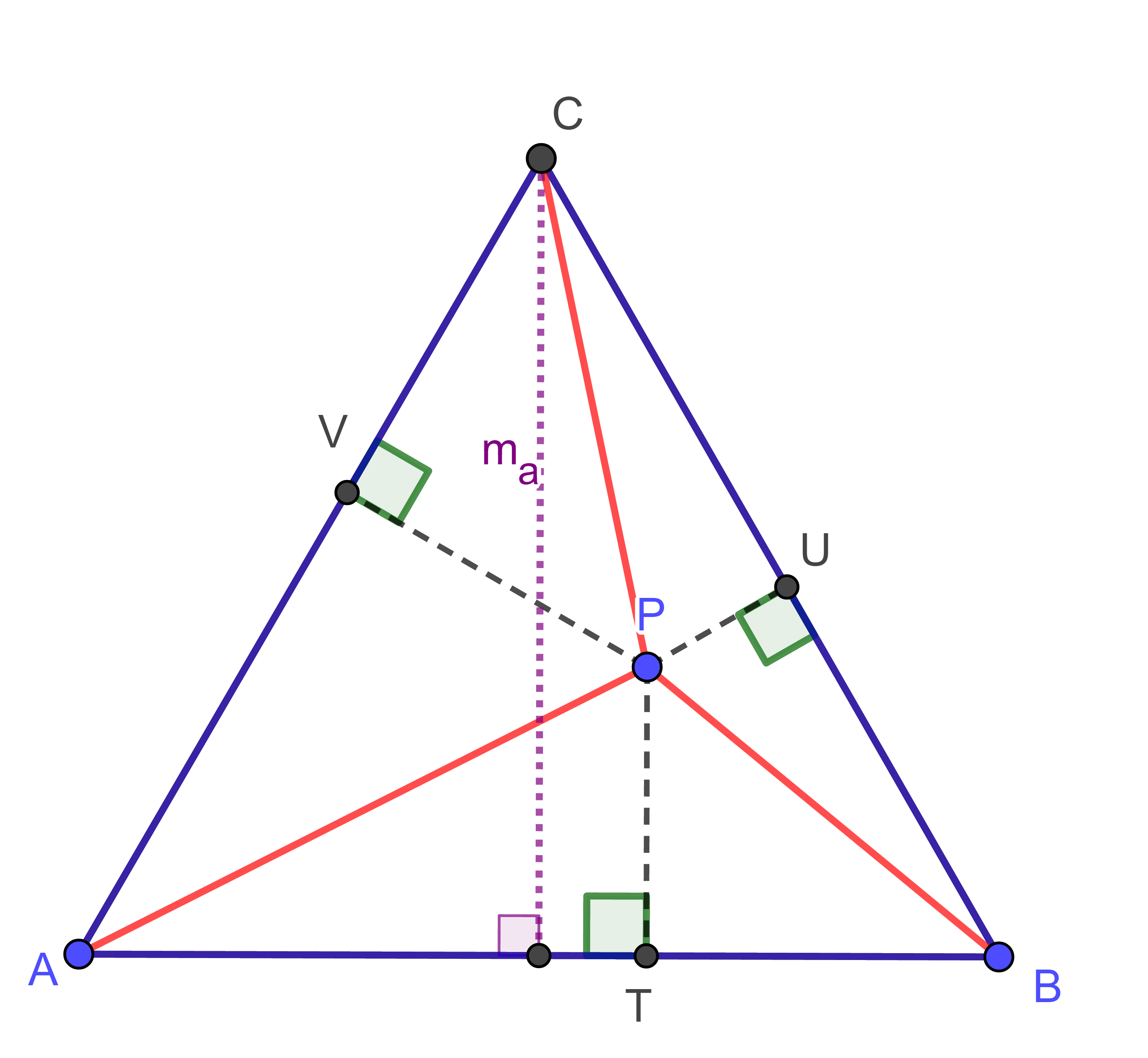
| Egy szabályos háromszög belsejében keressünk olyan pontot, amelynek a háromszög oldalaitól való távolságának összege a lehető legkisebb! |
| A
szabályos háromszög belsejében lévő bármely P pontnak az
oldalaktól mért távolságösszege mindig ugyanakkora, megegyezik a
háromszög magasságával.
Valóban,
hiszen ha az ABC
háromszög magasságát
azaz
és mivel AB=BC=CA,
ezért mindkét oldalt AB-vel
elosztva
|
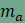
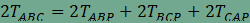 ,
,