Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
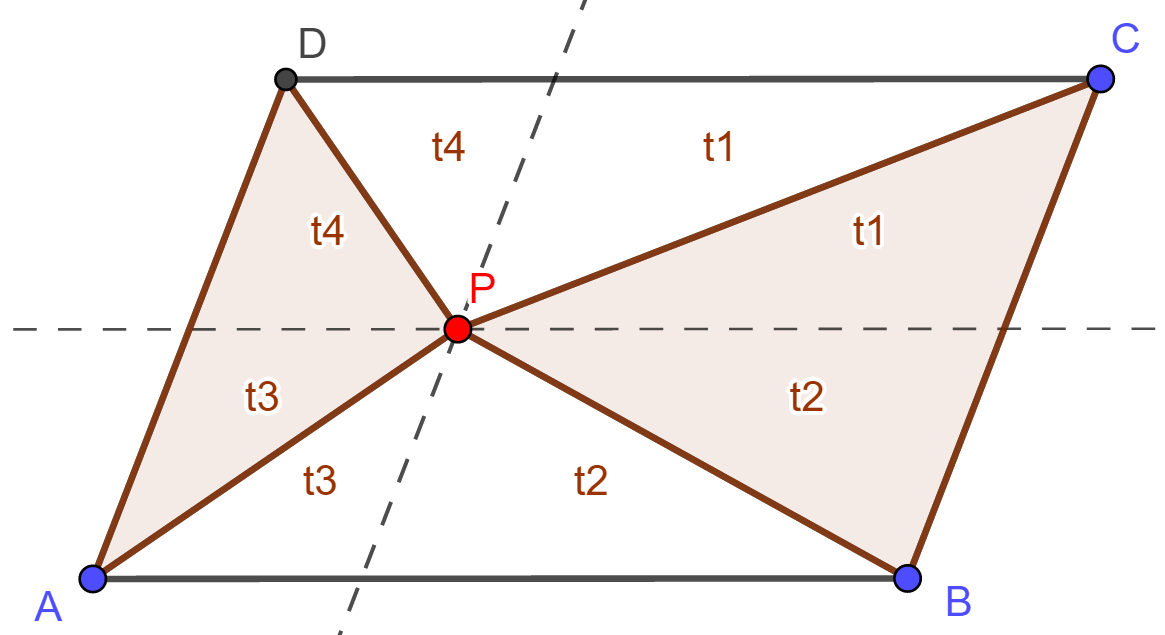
| Az ABCD paralelogramma belsejében kijelölünk egy P pontot. A P pontot összekötjük a paralelogramma csúcsaival. Mit állíthatunk a BCP és az ADP háromszögek területéről? |
| A
szerkesztés tanulmányozása után megfogalamzhatunk egy sejtést, amely
alapján a BCP
és ADP
háromszögek területének összege a P
pont helyzetétől függetlenül állandó, pont a paralelogramma területének
fele. Ennek belátásához húzzunk a P ponton át párhuzamost a paralelogramma oldalaival! Ezzel a paralelogrammát négy kisebb paralelogrammára bontottuk, amelyekben a PA, PB, PC és PD szakaszok egy-egy átlót alkotnak. A paralelogramma átlója megfelezi a paralelogramma területét, ezért az ábrán azonos módon megjelölt háromszögek területe megegyezik. Összegezve a megfelelő háromszögek területét láthatjuk, hogy a BCP és ADP háromszögek területösszege megegyezik az ABP és CDP háromszögek területösszegével. A fentiekből könnyen adódik, hogy a BCP és ADP háromszögek területének összege a P ponttól függetlenül állandó.
|