| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
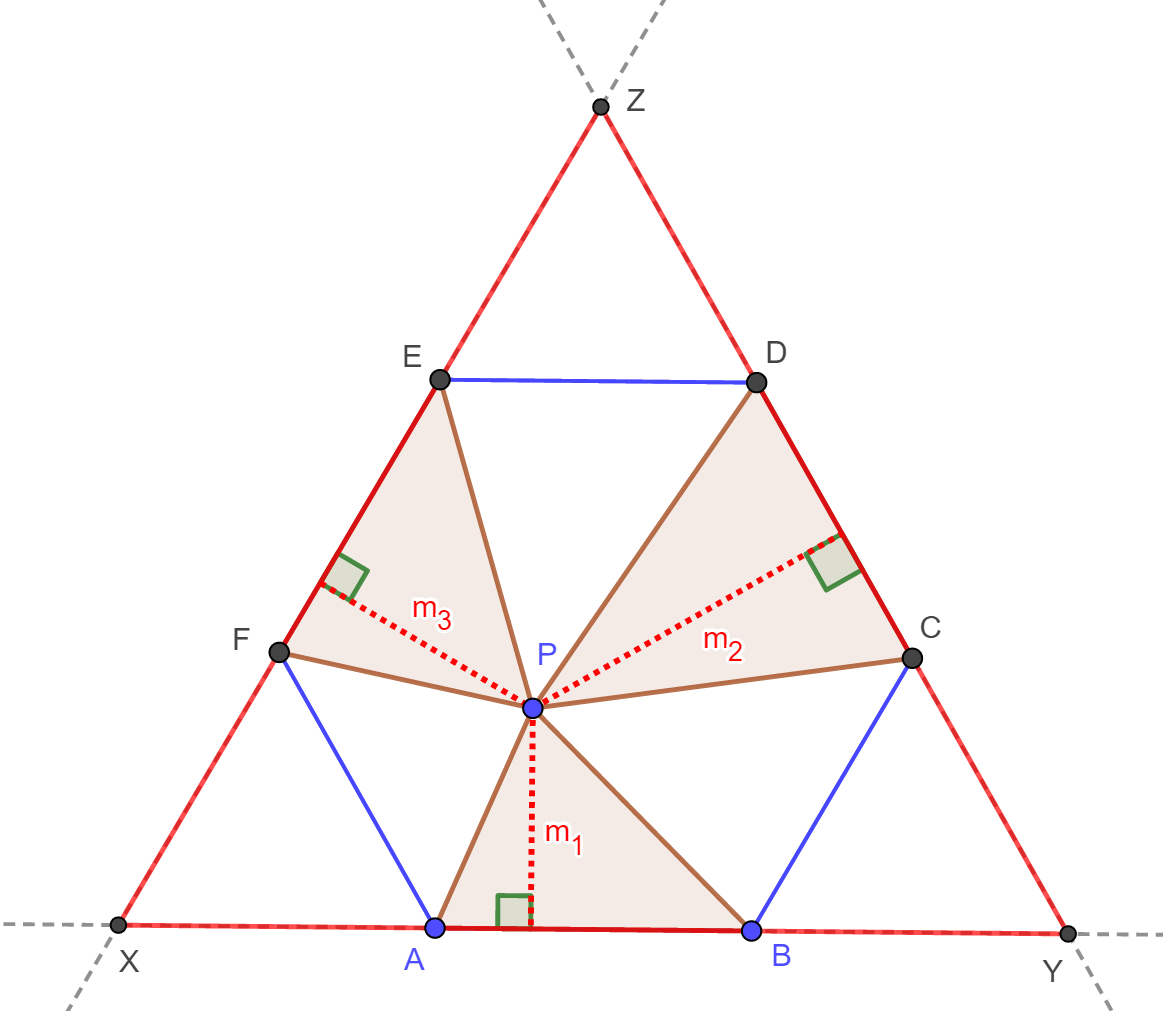
| Az ABCDEF szabályos hatszög belsejében kijelölünk egy P pontot. A P pontot összekötjük a hatszög csúcsaival, így a hatszöget háromszögekre bontjuk. Minden második háromszöget, azaz az ABP, CDP és EFP háromszögeket besatírozzuk. Mely P pontokra lesz maximális, illetve minimális a besítorozott háromszögek területösszege? |
A P
pont helyzetének változtatása mellett megfigyelhetjük, hogy a
satírozott háromszögek területösszege a P minden
helyzetében ugyanakkora. Ha a P
pontot a hatszög középpontjába visszük, akkor láthatjuk, hogy a
satírozott háromszögek területösszege ugyanakkora, mint a nem
satírozott háromszögek területösszege.
Ennek
bizonyításához egészítsük ki az ábrát! Húzzuk meg az
AB,
CD
és EF
egyeneseket, amik az alábbi ábra szerint az XYZ háromszöget
fogják
közre. A szabályos hatszög külső szögei 120°-osak, ezért az XYZ háromszög
szabályos. Most
húzzuk meg az ABP,
CDP
és EFP
háromszögek P
csúcsához
tartozó
A
fentiek alapján, ha az ABCDEF
szabályos
hatszög oldalának hosszát a
jelöli, akkor
ami
mutatja, hogy a satírozott
háromszögek területösszege valóban független a P pont helyzetétől. |

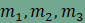 magasságát;
ezek egyben a
magasságát;
ezek egyben a 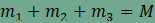 , ahol
, ahol