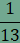| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
| Az ABCD paralelogramma AB és CD oldalát 4-4, BC és DA oldalát 3-3 egyenlő részre osztjuk, majd az ábra szerinti osztópontokat összekötjük. Milyen négyszög a QRST négyszög? Hányadrésze a QRST négyszög területe az ABCD paralegolramma területének? |
| Vizsgáljuk
meg a Forgatás nevű
csúszka segítségével a PQRS
négyszög szimmetria-tulajdonságait! Milyen
következtetések vonhatók le ebből a PQRS négyszögre? Az 1.eltolás, majd a 2.eltolás nevű csúszkák segítségével határozzuk meg a két négyszög területének arányát!
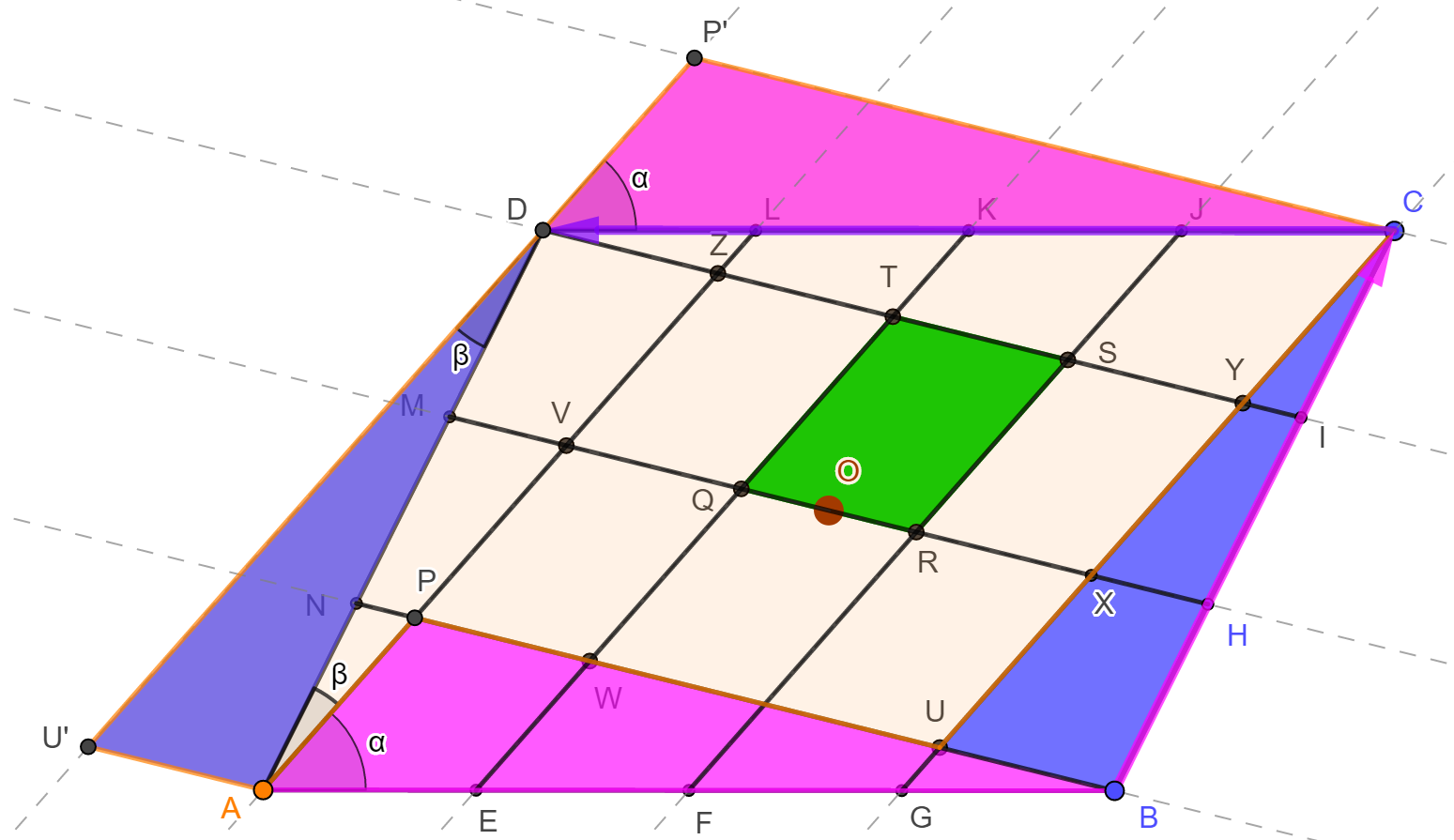
A Forgatás csúszka animálása mellett tanulmányozhatjuk az ábra szimmetria-tulajdonságait. A paralelogramma O középpontja körüli 180°-os forgatás a paralelogrammát természetesen önmagába viszi, de az egész ábra invariáns marad. Pontosabban a szemközti oldalakat összekötő szakaszok egymásba mennek át (konkrétan AL és CG, EK és JF, DI és BN egymás képe, míg HM önmagába megy át). Mivel a középpontos tükrözés egyenest önmagával párhuzamos egyenesbe visz, ezért az ABCD paralelogramma szemközti oldalait összekötő szakaszok egymással (AL, EK, FJ és GC, illetve BN, HM és ID) párhuzamosak. Ezt másképp úgy is megfogalmazhatjuk, hogy a fenti ábra színes négyszögei mind paralelogrammák. Megjegyezzük, hogy AL és EK párhuzamossága abból következik, hogy az AEKL négyszög paralelogramma (AE=LK és párhuzamosak). Tovább elemezve az O pontra vonatkozó középpontos tükrözést, megfigyelhetjük, hogy az ábra színes paralelogrammáinak mi a tükörképe (ld. alábbi ábra).
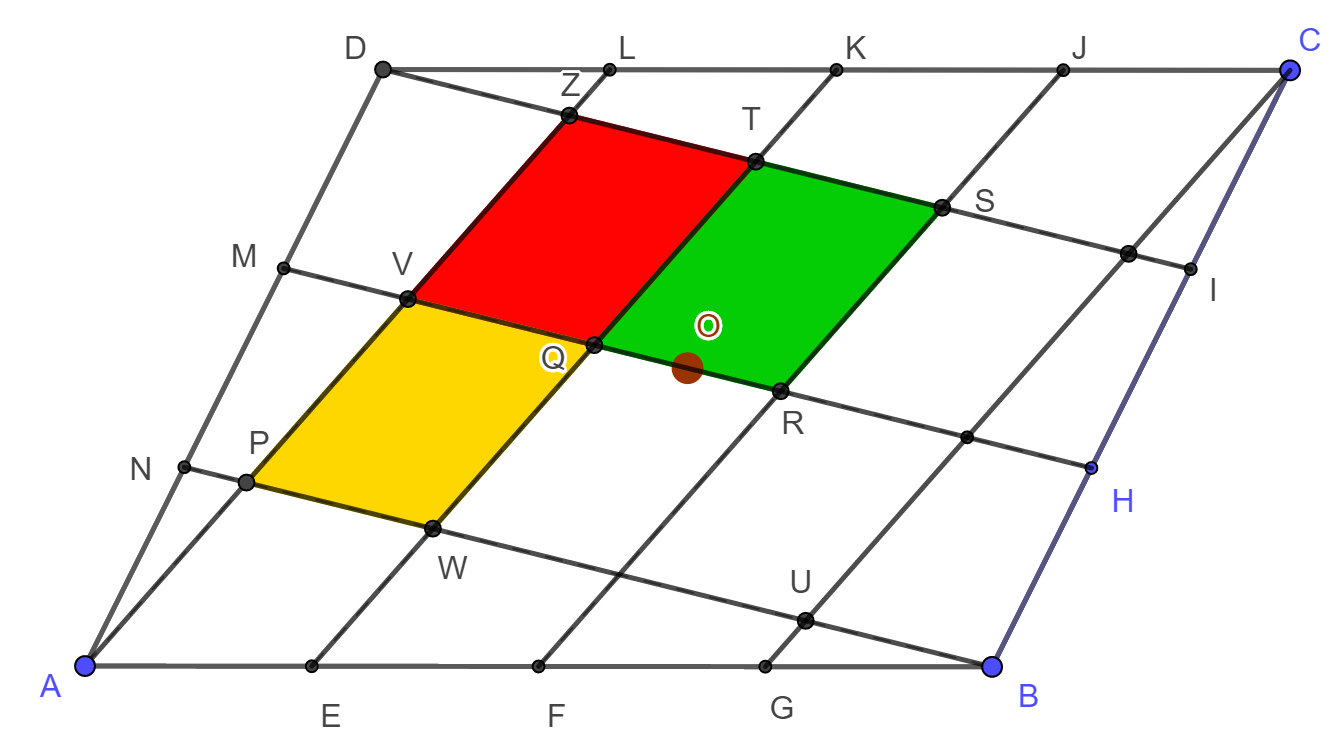
Mivel a PV szakasz képe YX, ezért PV=YX, vagyis az ábra piros és sárga paralelogrammái szögeikben és oldalaikban is megegyeznek, így egybevágók egymással. Végül az LJSZ trapézban K az egyik szár felezőpontja, továbbá KT párhuzamos a trapéz alapjaival, ezért KT szükségképpen a trapéz (szárakat összekötő) középvonala, amiből következik, hogy T a ZS szár felezőpontja, azaz ZT=TS. Ez azt is mutatja, hogy a zöld paralalelogrammák is egybevágók a piros és sárga paralalogrammákkal. Végül
az ABP és
a BCU
háromszögek eltolt képét vizsgáljuk. Toljuk el az ABP háromszöget
a
azaz az U’,
D
és P’
pontok egy egyenesre
illeszkednek. Ez azt is jelenti, hogy az ABCD paralelogramma
átdarabolható az
APUCP’U’
(konkáv) hatszöggé, amely viszont a QRST
paralelogrammákkal egybevágó
paralelogrammákból állítható össze. Mivel a felbontásban 13
paralelogramma
található, ezért a QRST
és az ABCD
paralelogrammák területének aránya
|
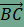, a 
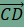vektorral.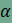 
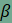-val
jelölt szögek,
hiszen váltószögek. Ezért a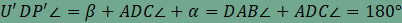 
,
