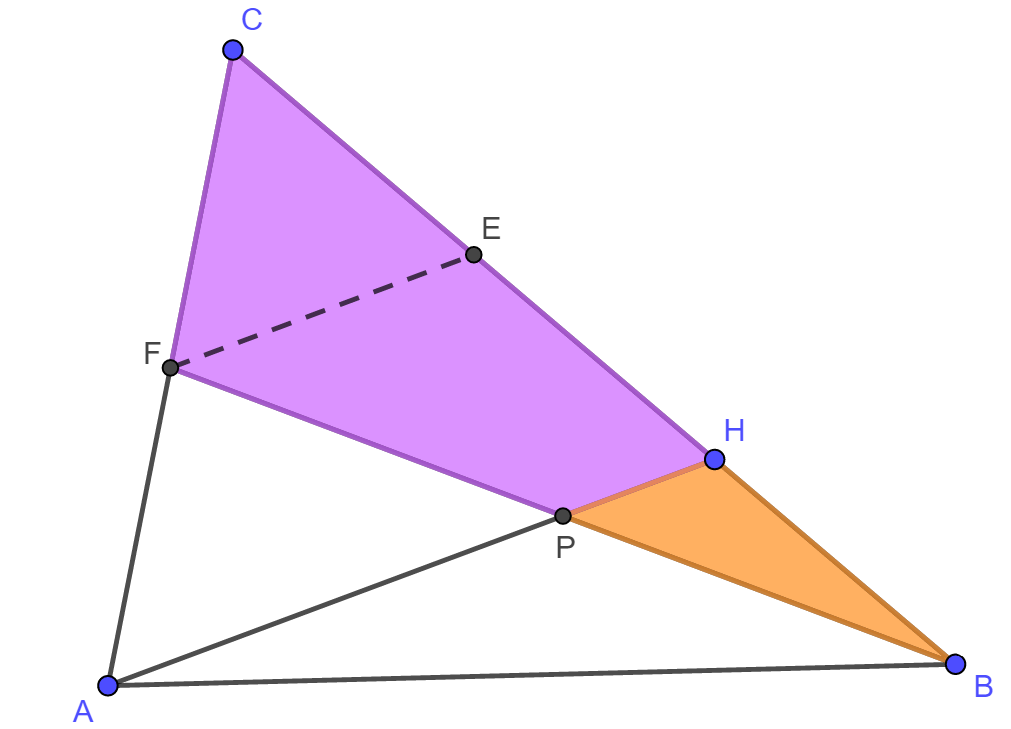
A háromszög C csúcsának
mozgatása, valamint a két sokszög területe alapján megfogalmazható
sejtés szerint a CFPH
négyszög területe 5-szöröse a BPH
háromszög területének. Erről a megfelelő jelölőnégyzet aktiválása után
meg is győződhetünk.
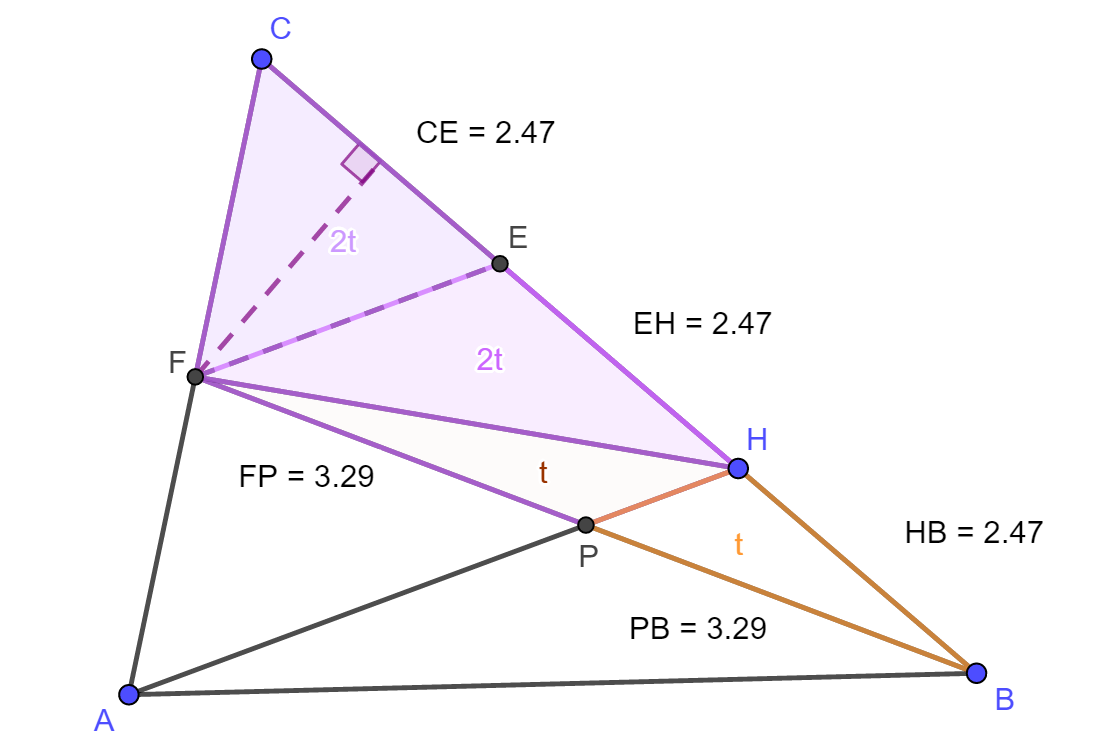
A sejtés bizonyításához vegyük észre, hogy a P pont mindig
ugyanabban az arányban osztja fel a BF szakaszt.
A P pont a BF szakaszt mindig
megfelezi. Ennek belátásához legyen E az CB szakasz C-hez közelebbi
harmadolópontja. Így EF
középvonal az AHC
háromszögben, ezért EF párhuzamos
AH-val.
Mivel pedig H
felezőpont a BEF háromszög BE oldalán, és PH párhuzamos EF-fel, ezért PH szükségképpen
középvonal ebben a háromszögben, amiből következik, hogy P valóban a BF szakasz
felezőpontja.
A
háromszög súlyvonalának ismert tulajdonsága, hogy megfelezi a háromszög
területét, és az előbb láttuk, hogy HP súlyvonal a BFH háromszögben,
ezért a BPH
és az FPH
háromszögek területe megegyezik (az alábbi ábrán t jelöli). Az E és H pontok
harmadolópontok a BC
oldalon, amit úgy is értelmezhetünk, hogy a BHF, EHF és CEF
háromszögeknek egy-egy oldala ugyanakkora. Ezekben a háromszögekben a
megegyező oldalakhoz ugyanakkora magasság tartozik, így a három
háromszög területe is megegyezik. Mivel a BHF háromszög
területe 2t,
ezért a másik két háromszög területe is ugyanekkora. Az ábra alapján
már látható, hogy a CFPH
négyszög és a BPH
háromszög területének aránya 5.
|