| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
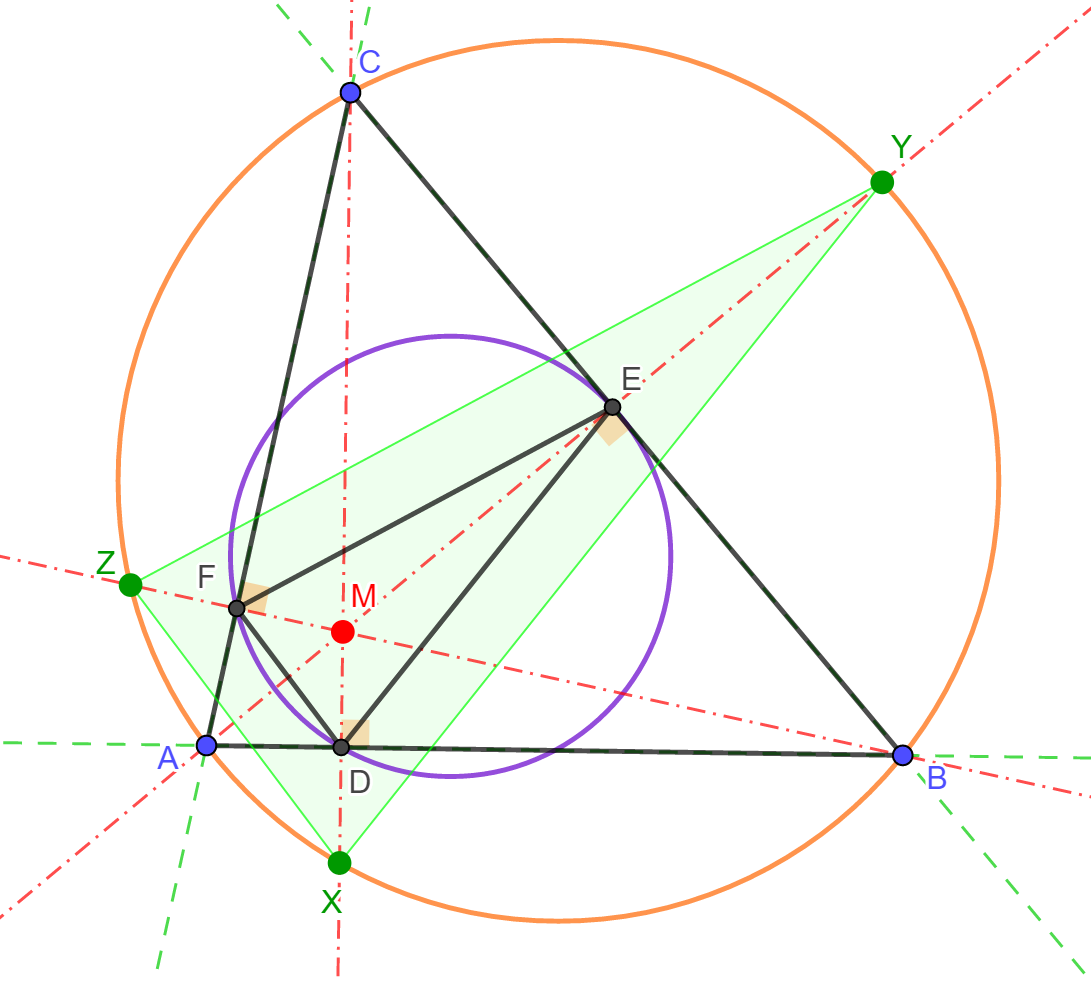
A hegyesszögű ABC háromszög M magasságpontját tükrözzük a háromszög AB, BC, CA oldalegyeneseire, a tükörképek rendre X, Y és Z.
összeg értékét! |
|
Az XYZ háromszög köré írt kör egybeesik az ABC háromszög köré írt körrel, vagy más megfogalmazásban a hegyesszögű háromszög magasságpontjának oldalegyenesekre vonatkozó tükörképe illeszkedik a háromszög köré írt körre. Ennek belátásához tekintsük az ABC háromszög DEF talpponti háromszögét. A DEF háromszög köré írt kör megegyezik az ABC háromszög Feuerbach-körével. A tükrözés tulajdonságai miatt a D, E és F pontok felezik az MX, MY és MZ szakaszokat, vagy más megközelítésben az XYZ háromszög a DEF háromszög kétszeresére nagyított képe az M pontra vonatkozóan. Ebből persze az is következik, hogy az XYZ háromszög köré írt kör az ABC háromszög Feuerbach körének kétszeresére nagyított képe, szintén az M pontra vonatkozóan. Ez a kör pedig pont az ABC háromszög köré írt körrel azonos, azaz X, Y és Z valóban illeszkedik az ABC háromszög köré írt körre.
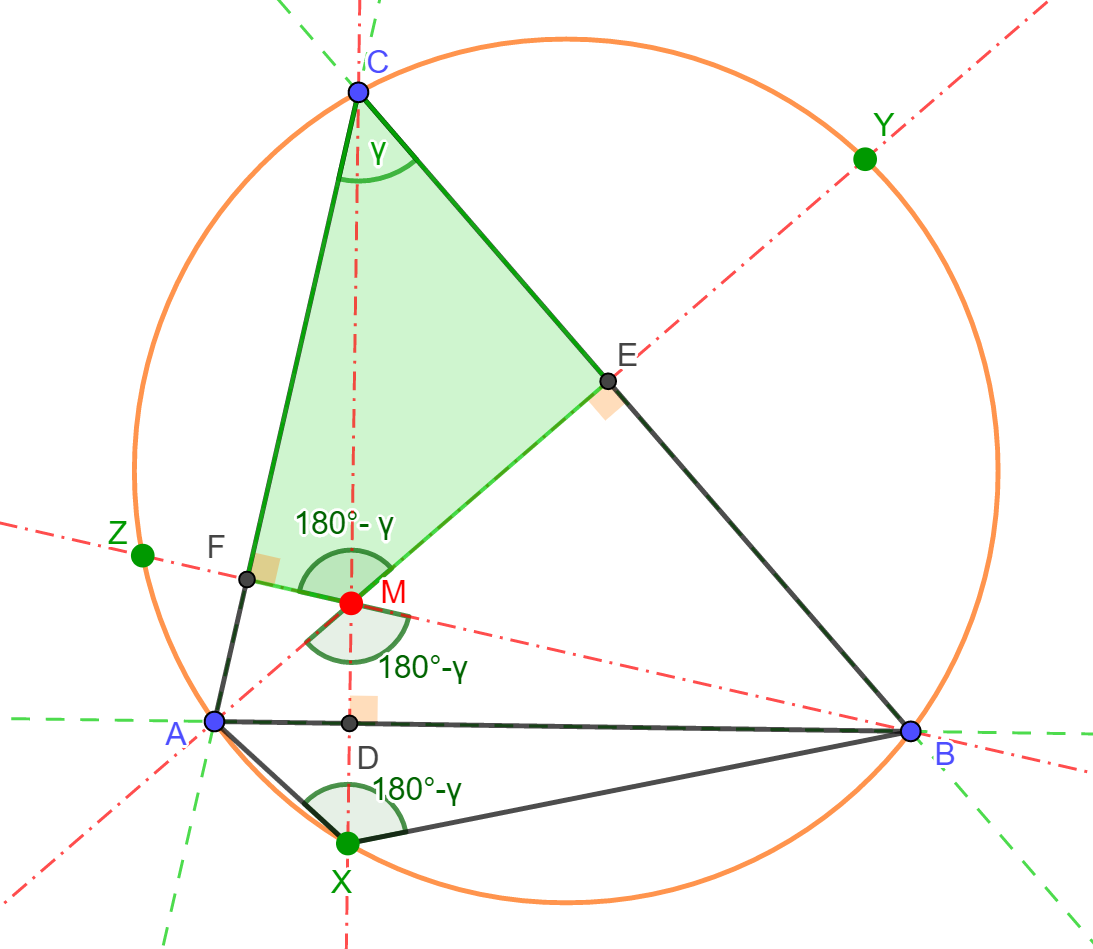
Megjegyezzük, hogy a fenti észrevételt az alábbi módszerrel is szokták igazolni. A CFME négyszögben az E és F csúcsoknál derékszög van, ezért húrnégyszög. Ebből adódik, hogy ha 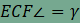 , akkor , akkor 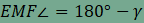 . Innen könnyen
beláthatjuk, hogy . Innen könnyen
beláthatjuk, hogy 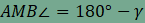 is
teljesül, lévén csúcsszöge az is
teljesül, lévén csúcsszöge az 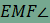 -nek. A tükrözés
szögtartó tulajdonságából azzonal következik, hogy -nek. A tükrözés
szögtartó tulajdonságából azzonal következik, hogy 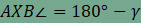 , és így a CAXB négyszögben a C és X csúcsoknál lévő
szögek összege 180°, azaz húrnégyszög. Ez azt jelenti, hogy X valóban az ABC háromszög köré
írt körén található. Ugyanígy látható be, hogy Y és Z is a körvonal
egy-egy pontja. , és így a CAXB négyszögben a C és X csúcsoknál lévő
szögek összege 180°, azaz húrnégyszög. Ez azt jelenti, hogy X valóban az ABC háromszög köré
írt körén található. Ugyanígy látható be, hogy Y és Z is a körvonal
egy-egy pontja.
A feladat második részében szereplő összeg minden hegyesszögű háromszögben 4, amint arról az animáció segítségével is meggyőződhetünk. Végezzük el a következő átalakításokat: 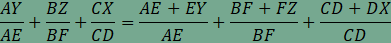 , ,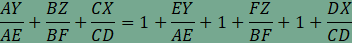 , ,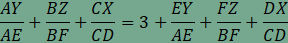 , ,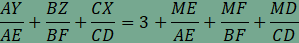 . .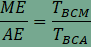 , ,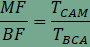 , ,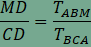 . .Visszaírva a területek arányát a keresett összegbe 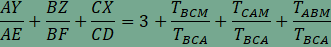 , ,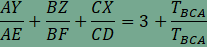 , ,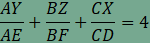 . .Ezzel az állítást beláttuk. |