Egy háromjegyű  $A$  szám rímelő, ha  $A$  minden pozitív egész kitevőjű hatványa  $A$  -ra végződik. Mennyi a rímelő számok összege?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Mennyi a háromjegyű palindromszámok átlaga?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az  $f: N\rightarrow N$  függvényre  $f(1)=1, f(2n)=f(n),f(2n+1)=f(2n)+1$  bármely pozitív egész  $n$  esetén. Határozzuk meg az  $f$  függvény maximumát, ha  $ 1\leq n \leq 5012$  .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

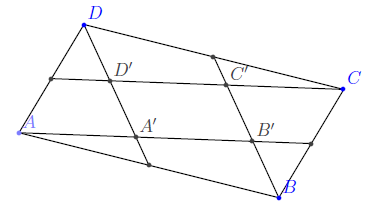
Egy adott  $ABCD$  paralelogramma oldalait osszuk fel az óramutató járásával ellentétes irányban haladva ciklikusan  $k:l$  arányban és az osztópontokat kössük össze az azonos körüljárás szerinti harmadik csúccsal. Mekkorának kell választanunk a  $k:l$  arányt, hogy a keletkező  $A'B'C'D'$  paralelogramma területe egytizenharmad része legyen a megadott  $ABCD$  paralelogramma területének?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy  $ 3$-reguláris egyszerű gráfban minden kör legalább hat élet tartalmaz. Legalább hány csúcsa van a gráfnak?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Határozzuk meg az

egyenlet egész megoldásai közül azt, amelyre maximális lesz az  $|y-x|$  értéke. Mennyi ez a maximum?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az Óperenciás tengeren is túl, az üveghegyen kerül megrendezésre a "Lábasfejűek Nemzetközi Konferenciája". A konferencia résztvevői -összesen 14 lábasfejű - a hegy lábánál gyülekeznek, lábaik száma rendre: 18, 22, 22, 24, 28, 30, 30, 30, 30, 32, 36, 36, 38, 38. Az üveghegy fala rendkívül csúszós; ahhoz, hogy egy lábasfejű feljuthasson, speciális mászócipőt kell húznia legalább minden második lábára. A lények (megfelelő számú cipő viselése mellett) fel és le közlekedhetnek a hegyen, de a cipőket kizárólag lábon szállíthatják. Legalább hány mászócipő szükségeltetik a feljutáshoz?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az  $ABC\triangle$  belső pontja  $P$  . Az  $AP$  egyenes a  $BC$  oldalt  $A_{1}$  -ben, a  $BP$  egyenes az  $AC$  oldalt  $B_{1}$  -ben metszi. Az  $APB_{1}\triangle$  területe 7, a  $BPA\triangle$  területe 8, az  $A_{1}PB\triangle$  területe pedig 9. Mekkora az  $ABC\triangle$  területe?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Hányféleképpen lehet  $ 2$  fekete,  $ 3$  fehér és  $ 4$  piros, a színtől eltekintve egyforma golyót egy sorban úgy elhelyezni, hogy fekete golyó ne kerüljön fehér mellé?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adjuk meg az alábbi egyenlet legkisebb és legnagyobb gyökének szorzatát  $p/q$  alakban, ahol a tört már nem egyszerűsíthető. Mennyi lesz a  $|p|+|q|$  értéke?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy  $d = \sqrt{1001} + \sqrt{999}$  átmérőjű  $k$  körbe két kört írunk, amelyek kívülről érintik egymást és mindketten érintik a  $k$  kört is. A három kör középpontja egy egyenesre esik. A két beírt kör közös belső érintőjének a  $k$  belsejébe eső szakasza  $\sqrt{2000}$  hosszúságú. A két beírt kör összesen  $\pi\cdot A$  területű részét nem fedi le a k körnek. Mennyi az  $A$  értéke?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy téglatest egy csúcsba futó éleinek hossza  $ 7, 14$  és  $ 21$  egység. Adjuk meg annak a szomszédos lapokon elhelyezkedő két kitérő lapátlónak a távolságnégyzetét, amelyekre ez a távolság maximális.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

 $ 100$  cédulára felírtuk a pozitív egészeket  $ 1$  -től  $ 100$  -ig és betettük a cédulákat egy dobozba. A dobozból egyesével, visszatevés nélkül cédulákat húzunk. A húzás akkor ér véget, ha a kihúzott számok között  $ 6$  különböző szerepel. Jelöljük  $X(i)$  -vel az  $i$  -edik olyan kihúzott számot, amelyik minden korábbitól különbözik. Az  $X(i)$  értéket rekordnak nevezzük, ha minden korábban kihúzott számnál nagyobb. Határozzuk meg az  $X(1), X(2), \dotsX(6)$  sorozatban a rekordok számának várható értékét tovább nem egyszerűsíthető törtalakban. Mennyi e tört számlálójának és nevezőjének szorzata?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy kör az  $y=x^{2}$  egyenletű parabolát két pontban metszi és egy pontban érinti. A két metszéspont abszcisszája  $x_{1}=-888$  és  $x_{2}=-3104$  . Határozzuk meg az érintési pont abszcisszáját.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

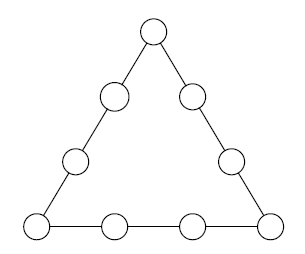
Az ábrán látható háromszög oldalai mentén az üres körökben elhelyeztük az egyjegyű pozitív számok négyzeteit, mindegyiket egyszer felhasználva úgy, hogy a háromszög bármely oldala mentén ugyanakkora lett a négy szám összege. Mennyi a csúcsokba írt számok összege?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Van 64 darab páronként különböző tömegű érménk. Egy kétkarú mérleg segítségével ki akarjuk választani a legkönnyebbet és a második legnehezebbet. Mennyi a legkevesebb mérés, amellyel ez biztosan sikerül?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy négyszög három egymás után következő oldalának hossza rendre  $ 29, 10$  , illtve  $ 17$  méter. Adva van még az első két megadott oldal által bezárt szög tangense  $tg\alpha=\dfrac{21}{20}$  , továbbá a második és harmadik oldal által bezárt szög szinusza  $sin\beta=-\dfrac{8}{17}$  . Mekkora a negyedik oldal négyzete?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A  $ 0$  -tól  $ 8$  -ig számozott dominókból Annának teljes készlete van. (A készletben vannak az üres-üres,  $ 1-1,\ldots , 8-8$  darabok is, és minden fajtából csak egyetlen darab van.) Anna találomra kiválaszt egy dominót, majd a maradékok közül Béla véletlenszerűen húz kettőt. Jelölje  $p/q$  annak a valószínűségét, hogy Béla dominói párosíthatók. (  $p, q$  pozitív egész számok és relatív prímek.) Mennyi  $p+q$  értéke?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy  $a, b, c$  oldalú háromszög körülírt körének sugara  $R$  . Ismeretes, hogy két olyan, egymáshoz nem hasonló  $H_1$  és  $H_2$  háromszög létezik, amelyekben  $ R=a-b$  és $R^{2}=ab$. Hány fok  $H_1$  és  $H_2$  legnagyobb szögének összege?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy tetraéder minden csúcsában egy-egy  $ 5, \sqrt{34}$  és egy  $\sqrt{41}$  hosszúságú él találkozik. Mekkora a tetraéder térfogata?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba