Az $ ABCD $ húrtrapéz köré írt körének egyenlete $ ( x - 3 )^2 + ( y - 2)^2 = 100 $ . A húrtrapéz szimmetriatengelyének egyenlete $ 2x - y = 4 $. A trapéz $ AB $ alapjának egy belső pontja $ P(-5; 1) $, $ BC $ szárának hossza pedig $ 10 \sqrt{ 2 } $ egység. Határozza meg a trapéz csúcsainak koordinátáit!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 1 méter oldalú négyzetbe egy második négyzetet rajzoltunk úgy, hogy a belső négyzet minden csúcsa illeszkedjen a külső négyzet egy-egy oldalára. A belső és a külső négyzet oldalainak aránya 5 : 7.

a) Milyen arányban osztja két részre a belső négyzet csúcsa a külső négyzet oldalát? Az arány pontos értékét adja meg!

A belső négyzetbe egy újabb, harmadik négyzetet rajzolunk úgy, hogy a harmadik és a második négyzet oldalainak aránya is 5 : 7. Ezt az eljárást aztán gondolatban végtelen sokszor megismételjük.

b) Mekkora lesz a kapott négyzetek kerületeinek az összege, ha a kiindulási négyzet kerülete is tagja a (végtelen sok tagú) összegnek?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy üzemben olyan forgáshenger alakú konzervdoboz gyártását szeretnék elkezdeni, Ft amelynek térfogata 1000 cm3. A doboz aljának és tetejének anyagköltsége $ 0,2 \dfrac{Ft}{cm^2} $ míg oldalának anyagköltsége $ 0,1 \dfrac{Ft}{cm^2} $

a)Mekkorák legyenek a konzervdoboz méretei (az alapkör sugara és a doboz magassága), ha a doboz anyagköltségét minimalizálni akarják? Válaszát cm-ben, egy tizedesjegyre kerekítve adja meg! Számítsa ki a minimális anyagköltséget is egész forintra kerekítve!

A megtöltött konzervdobozokat tizenkettesével csomagolták kartondobozokba. Egy ellenőrzés alkalmával 10 ilyen kartondoboz tartalmát megvizsgálták. Minden kartondoboz esetén feljegyezték, hogy a benne található 12 konzerv között hány olyat találtak, amelyben a töltősúly nem érte el az előírt minimális értéket. Az ellenőrök a 10 kartondobozban rendre 0, 1, 0, 0, 2, 0, 0, 1, 3, 0 ilyen konzervet találtak, s ezeket a konzerveket selejtesnek minősítették.

b) Határozza meg a kartondobozonkénti selejtes konzervek számának átlagát és az átlagtól mért átlagos abszolút eltérését!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy építőkészletben a rajzon látható négyzetes hasáb alakú elem is megtalálható. Két ilyen építőelem illeszkedését az egyik elem tetején kiemelkedő négy egyforma kis henger és a másik elem alján lévő nagyobb henger szoros, érintkező kapcsolata biztosítja. (Ez azt jelenti, hogy a hengerek tengelyére merőleges síkmetszetben a nagyobb kört érinti a négy kisebb kör, amelyek középpontjai egy négyzetet határoznak meg.) Tudjuk, hogy a kis hengerek sugara 3 mm, az egymás melletti kis hengerek tengelyének távolsága pedig 12 mm.

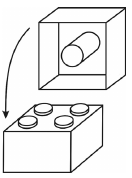
a) Mekkora a nagyobb henger átmérője? Válaszát milliméterben, két tizedesjegyre kerekítve adja meg!

A készletben az építőelemek kék vagy piros színűek. Péter 8 ilyen elemet egymásra rak úgy, hogy több piros színű van köztük, mint kék. Lehet, hogy csak az egyik színt használja, de lehet, hogy mindkettőt.

b) Hányféle különböző színösszeállítású 8 emeletes tornyot tud építeni?

A gyárban (ahol ezeket az építőelemeket készítik) nagyon ügyelnek a pontosságra. Egymillió építőelemből átlagosan csupán 20 selejtes. András olyan készletet szeretne vásárolni, melyre igaz a következő állítás: 0,01-nál kisebb annak a valószínűsége, hogy a dobozban található építőelemek között van selejtes.

c) Legfeljebb hány darabos készletet vásárolhat András?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy dobozban 17 darab egyforma sugarú golyó van. A golyók közül 8 darab sárga és 9 darab zöld.

a) Visszatevés nélkül kihúzunk a dobozból 3 golyót. Mennyi annak a valószínűsége, hogy a kihúzott 3 golyó egyszínű?

b) Ha úgy húzunk ki a dobozból 5 golyót, hogy a kivett golyót minden egyes húzás után visszatesszük, akkor mennyi annak a valószínűsége, hogy 3 alkalommal sárga golyót, 2 alkalommal pedig zöld golyót húzunk?

c) A golyók meg vannak számozva 1-től 17-ig. Mennyi annak a valószínűsége, hogy visszatevés nélkül 3 golyót kihúzva a golyókon található számok összege osztható 3-mal?

Válaszait három tizedesjegyre kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba