a) Egy téglalapot 720 darab egybevágó kis téglalapra daraboltunk szét. A kis téglalapok oldalai közül az egyik 1 cm-rel hosszabb, mint a másik. Hány cm hosszúak egy-egy kis téglalap oldalai, ha a nagy téglalap területe $ 2025\ cm^2 $ ?

b) Az 1, 2, 3, 4, 5, 6 számjegyekből összesen 720 olyan hatjegyű szám képezhető, melynek számjegyei között nincsenek egyenlők. Ezek között hány 12-vel osztható van?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Jelölje $ H $ a $ \sqrt{ 5,2 - x } \le 3 $ egyenlőtlenség pozitív egész megoldásainak halmazát. Jelölje továbbá $ B $ azon pozitív egész $ b $ számok halmazát, amelyekre a$ \log_b 2^6 $ kifejezés értéke is pozitív egész szám. Elemeinek felsorolásával adja meg a $ H $, a $ B $, a $ H \cap B $ és a $ B \setminus H $ halmazt!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy cég a függőleges irány kijelölésére alkalmas, az építkezéseknél is gyakran használt „függőónt” gyárt, amelynek nehezéke egy acélból készült test. Ez a test egy 2 cm oldalhosszúságú szabályos ötszög egyik szimmetriatengelye körüli forgatásával származtatható.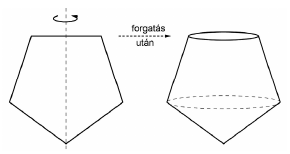

a)Hány cm 3 a nehezék térfogata? Válaszát egy tizedesjegyre kerekítve adja meg!

A minőségellenőrzés 120 darab terméket vizsgált meg. Feljegyezték az egyes darabok egész grammokra ke rekített tömegét is. Hatféle tömeg fordult elő, ezek relatív gyakoriságát mutatja az oszlopdiagram.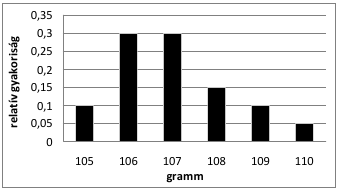

b) Készítsen gyakorisági táblázatot a 120 adatról, és számítsa ki ezek átlagát és szórását!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Megoldás:

a) a $ ]–2; –1] $-on (szigorúan monoton) növekvő;
az $ x = -1 $ helyen (helyi) maximuma van, amelynek értéke 3,5;
a $ [–1; 2] $-on (szigorúan monoton) csökkenő;
az $ x = 2 $ helyen (helyi) minimuma van, amelynek értéke -10;
a $ [2; 3[ $-on (szigorúan monoton) növekvő.

b) $ g ( x) = \dfrac{x^4}{4}-\dfrac{x^3}{2}-3x^2+12  $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba