Tekintsük az $ (a_n) $ sorozatot: $ a_1 = \dbinom{2}{2} = 1 $, $ a_2 = \dbinom{3}{2} = 3 $, $ a_3 = \dbinom{4}{2} = 6 $ és így tovább, $ a_n = \dbinom{n+1}{2} $

a) Számítsa ki az $ (a_n) $ sorozat első öt tagjából álló számsokaság átlagát és szórását!
b) A fenti $ (a_n) $ sorozatból képezzük a $ (b_n) $ sorozatot: $ b_n = \dfrac{a_{n+1}}{a_n} $. Mennyi a $ (b_n) $ sorozat határértéke?
A $ (c_n) $ számtani sorozat differenciája 0,25. A sorozat első n tagjának összege 100, első $ 2n $ tagjának összege 300 ($ n \in \mathbb{N}^+ $).
c) Határozza meg $ n $ értékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ókori egyiptomiak az egyenlő szárú háromszög területét (közelítő módszerrel) úgy számolták ki, hogy az alap és a szár szorzatának a felét vették.
a) Egy egyenlő szárú háromszög alapja 18 cm hosszú. Mekkora lehet a szára, ha az ókori egyiptomiak módszere e háromszög valódi területét 25\%-nál kisebb hibával adja meg?
Az ókori Egyiptom matematikájában a számok négyzetének is jelentős szerep jutott.
b)Hány olyan 1000-nél kisebb pozitív egész szám van, amellyel az 1⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 számot megszorozva négyzetszámot kapunk?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A statisztikai értékelések során szükség van az adatokat és összefüggéseket szemléltető pontok és egyenesek kölcsönös helyzetének jellemzésére. Egy ilyen jellemző lehet a pontnak egy megadott egyenestől mért függőleges távolsága.

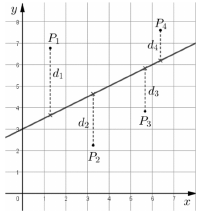Az ábrán látható $ P_1 $, $ P_2 $, $ P_3 $, $ P_4 $ pontok esetén a függőleges távolságok rendre a $ d_1 $, $ d_2 $, $ d_3 $, $ d_4 $ szakaszok hosszával egyenlők. (A távolságokat megadó szakaszok párhuzamosak az y tengellyel.)
a) Határozza meg az $ R(4; 2) $ és az $ S(4; 5) $ pontok függőleges távolságát az $ y = \dfrac{1}{3}x + \dfrac{5}{3}$ egyenestől!
Ha a derékszögű koordináta-rendszerben az adatokat pontokkal jelenítjük meg, és különböző egyeneseket veszünk fel, akkor mindegyik egyeneshez kiszámítható a pontok függőleges távolságainak négyzetösszege (az ábrán látható példában $ d_1^2 + d_2^2 + d_3^2 + d_4^2 $ ). Tekintsük azt az egyenest a pontokra legjobban illeszkedő egyenesnek, amelyre ez a négyzetösszeg a lehető legkisebb.
Adott három pont a koordináta-rendszerben: $ A(1; 3) $, $ B(3; 5) $ és $ C(4; 4) $.
b) Adja meg az m értékét úgy, hogy az $ y = mx $ egyenletű (origón átmenő) egyenes a megadott módszer szerint a legjobban illeszkedjen az $ A $, $ B $ és $ C $ pontokra! ($ m \in \mathbb{R} $)
Az $ y =\dfrac{1}{3} ( -2 x^2 + 11x) $ egyenletű $ g $ görbe áthalad a megadott $ A $ és $ B $ pontokon, a $ h $ egyenes pedig az origón és a $ C $ ponton.
c) Mekkora a $ g $ és $ h $ által közbezárt korlátos alakzat területe?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy áruházláncban minden Kocka csokoládé vásárlásakor a csoki mellé ajándékba adnak egy „zsákbamacska” csomagot, amelyben egy kis fémkocka van. A fémkocka mindegyik lapja sárga vagy kék színűre van festve úgy, hogy mind a két színű lap előfordul.
a) Igazolja, hogy (színezés szerint) összesen 8-féle kocka van, ha a forgatással egymásba vihető színezéseket nem tekintjük különbözőnek!
b) Dórinak 7 különböző színezésű kockája van, így már csak egy hiányzik a teljes készlethez, hogy abból nyakláncot készítsen magának. Mennyi annak a valószínűsége, hogy ha 3 darab Kocka csokoládét vesz, akkor meglesz a teljes készlete? (Feltételezhetjük, hogy mindegyik kockafajta ugyanakkora valószínűséggel fordul elő a csomagokban.)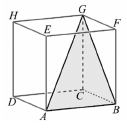

Az ábrán látható $ ABCDEFGH $ kocka élhosszúsága 10 egység.
c) Számítsa ki az $ ABG $ háromszög beírt körének sugarát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Két forgáshenger alakú viaszgyertyánk van. Az egyik gyertya alapkörének sugara $ r $, magassága $ h $, a másik alapkörének sugara $ R $, magassága szintén $ h $. A két gyertyát összeolvasztjuk, majd a viaszból egy ugyancsak $ h $ magasságú, forgáshenger alakú gyertyát öntünk ($ r, h, R > 0 $).
a) Igazolja, hogy az így kapott gyertya alapkörének sugara legalább $ \sqrt{2rR} $. (Az öntés során fellépő anyagveszteségtől eltekinthetünk.)
Egy forgáshenger alakú tortát egy 15 cm sugarú, félgömb alakú védőbúra alatt helyezünk el. A torta a félgömb határoló körének síkján áll, és a torta fedőlapjának határoló köre a félgömbre illeszkedik (az ábra szerint).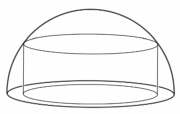

b) Igazolja, hogy az $ m $ cm magasságú torta térfogata (köbcentiméterben mérve) $ 225 π m − π m^3 $. ($ 0 < m < 15 $)
c) Igazolja, hogy a védőbúra alatt (a fent leírt módon) elhelyezhető maximális térfogatú torta térfogata kisebb, mint a félgömb térfogatának 60\%-a!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba