1. találat: Matematika középszintű érettségi, 2012. május, II. rész, 13. feladat
Témakör: *Algebra ( exponenciális, egyenlet, törtes) (Azonosító: mmk_201205_2r13f )
Oldja meg az alábbi egyenleteket a valós számok halmazán!
a) $ 5^{x+1}+5^{x+2}=30$
b) $\dfrac{3}{x}-\dfrac{2}{x+2}=1$, ahol $x \ne 0$ és $x \ne -2$
*Geometria ( terület, koszinusztétel, trapéz, hasonlóság) (Azonosító: mmk_201205_2r14f )
Az ABC hegyesszögű háromszögben BC = 14 cm, AC = 12 cm, a BCA szög nagysága pedig $ 40^{\circ}$.
a) Számítsa ki a BC oldalhoz tartozó magasság hosszát!
b) Számítsa ki az AB oldal hosszát!
Válaszait cm-ben, egy tizedesjegyre kerekítve adja meg!
Az AB oldal felezőpontja legyen E, a BC oldal felezőpontja pedig legyen D.
c) Határozza meg az AEDC négyszög területét! Válaszát $cm^2$-ben, egy tizedesjegyre kerekítve adja meg!
*Sorozatok (Azonosító: mmk_201205_2r15f )
Az újkori olimpiai játékok megrendezésére 1896 óta kerül sor, ebben az évben tartották az első (nyári) olimpiát Athénban. Azóta minden negyedik évben tartanak nyári olimpiát, és ezeket sorszámmal látják el. Három nyári olimpiát (az első és a második világháború miatt) nem tartottak meg, de ezek az elmaradt játékok is kaptak sorszámot.
a) Melyik évben tartották a 20. nyári olimpiai játékokat?
b) Számítsa ki, hogy a 2008-ban Pekingben tartott nyári olimpiának mi volt a sorszáma!
A nyári olimpiák szervezőinek egyik fő bevételi forrása a televíziós jogok értékesítéséből származó bevétel. Rendelkezésünkre állnak a következő adatok (millió dollárban számolva):

Eszter úgy véli, hogy a televíziós jogok értékesítéséből származó bevételek – a 20. olimpiától kezdve – az egymás utáni nyári olimpiákon egy számtani sorozat egymást követő tagjait alkotják. Marci szerint ugyanezek a számok egy mértani sorozat egymást követő tagjai. A saját modelljük alapján mindketten kiszámolják, hogy mennyi lehetett a televíziós jogok értékesítéséből származó bevétel a 27. nyári olimpián. Ezután megkeresik a tényleges adatot, amely egy internetes honlap szerint 1383 (millió dollár).
c) Számítsa ki, hogy Eszter vagy Marci becslése tér el kisebb mértékben a 27. nyári olimpia tényleges adatától!
*Halmazok ( metszet, Venn-diagram, valószínűségszámítás) (Azonosító: mmk_201205_2r16f )
Tekintsük a következő halmazokat:
A = $\{$a 100-nál nem nagyobb pozitív egész számok$\}$;
B = $\{$a 300-nál nem nagyobb 3-mal osztható pozitív egész számok$\}$;
C = $\{$a 400-nál nem nagyobb 4-gyel osztható pozitív egész számok$\}$.
a) Töltse ki a táblázatot a minta alapján, majd a táblázat alapján írja be az 52, 78, 124, 216 számokat a halmazábra megfelelő tartományába!
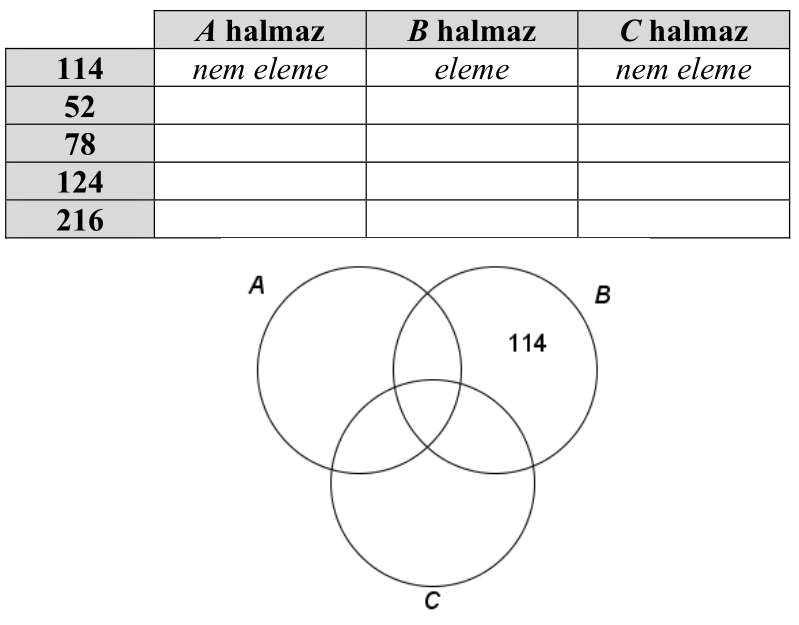
b) Határozza meg az $A \cap B \cap C$ halmaz elemszámát!
c) Számítsa ki annak valószínűségét, hogy az A halmazból egy elemet véletlenszerűen kiválasztva a kiválasztott szám nem eleme sem a B, sem a C halmaznak!
*Statisztika ( kombinatorika) (Azonosító: mmk_201205_2r17f )
Az alábbi táblázat András és Bea érettségi érdemjegyeit mutatja.
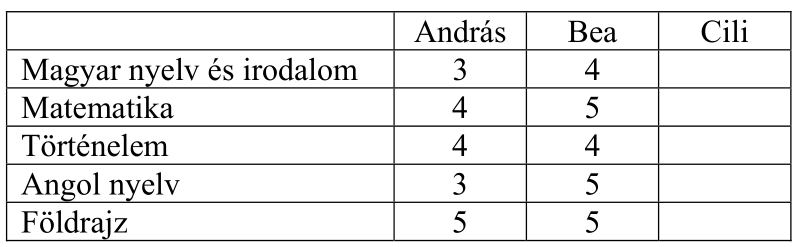
a) Számítsa ki András jegyeinek átlagát és szórását!
Cili érettségi eredményéről azt tudjuk, hogy jegyeinek átlaga András és Bea jegyeinek átlaga közé esik, továbbá Cili jegyeinek a szórása 0.
b) Töltse ki a táblázatot Cili jegyeivel!
Dávid is ebből az 5 tárgyból érettségizett, az 5 tárgy az ő bizonyítványában is a fenti sorrendben szerepel. Eredményeiről azt tudjuk, hogy jegyeinek mediánja 4, átlaga pedig 4,4 lett.
c) Határozza meg Dávid osztályzatait és azt, hogy hányféleképpen lehetne ezekkel az osztályzatokkal kitölteni az érettségi bizonyítványát!
Az ábra a 24 fős osztály érettségi eredményeinek megoszlását mutatja matematikából. Tudjuk, hogy jeles osztályzatot 4 tanuló ért el.
d) Az osztály tanulói közül hányan érettségiztek közepes eredménnyel matematikából?

*Térgeometria ( kombinatorika, gráfok, Pitagorasz-tétel, koszinusztétel, ) (Azonosító: mmk_201205_2r18f )
a) Számítsa ki annak a szabályos négyoldalú gúlának a térfogatát, melynek minden éle 10 cm hosszú!
Térgeometriai feladatok megoldásában segíthet egy olyan készlet, melynek elemeiből (kilyuggatott kisméretű gömbökből és különböző hosszúságú műanyag pálcikákból) matematikai és kémiai modellek építhetők. Az ábrán egy kocka modellje látható.
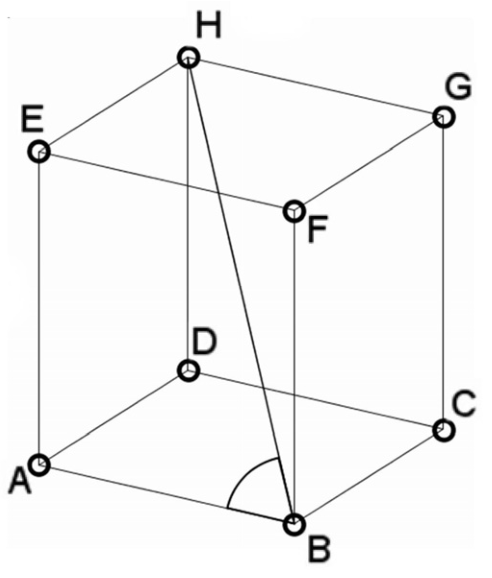
b) Számítsa ki az ABH szög nagyságát! (A test csúcsait tekintse pontoknak, az éleket pedig szakaszoknak!)
Anna egy molekulát modellezett a készlet segítségével, ehhez 7 gömböt és néhány pálcikát használt fel. Minden pálcika két gömböt kötött össze, és bármely két gömböt legfeljebb egy pálcika kötött össze. A modell elkészítése után feljegyezte, hogy hány pálcikát szúrt bele az egyes gömbökbe. A feljegyzett adatok: 6, 5, 3, 2, 2, 1, 1.
c) Mutassa meg, hogy Anna hibát követett el az adatok felírásában!
Anna is rájött, hogy hibázott. A helyes adatok: 6, 5, 3, 3, 2, 2, 1.
d) Hány pálcikát használt fel Anna a modell elkészítéséhez?


