Feladatbank keresés

Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

Látogatók

Összes:

10 719 582

Mai:

2 007

18-97-14-88.crawl.commoncrawl.org
(IP: 18.97.14.88)

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium

Óbudai Árpád Gimnázium

Szent István Gimnázium

Békásmegyeri Veres Péter Gimnázium

Első lap
1
Utolso lap

Találatok száma: 12 (listázott találatok: 1 ... 12)

1. találat: Matematika középszintű érettségi, 2013. október, I. rész, 1. feladat
Témakör: *Halmazok ( különbség) (Azonosító: mmk_201310_1r01f )

Megoldás:

A \ B = {-4; -3; -2; -1; 0}

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

2. találat: Matematika középszintű érettségi, 2013. október, I. rész, 2. feladat
Témakör: *Függvények (abszolútérték, algebra, egyenlet) (Azonosító: mmk_201310_1r02f )

Adott a valós számok halmazán értelmezett $f(x)=|x-4|$ függvény. Mely x értékek esetén lesz f(x)=6 ?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

3. találat: Matematika középszintű érettségi, 2013. október, I. rész, 3. feladat
Témakör: *Algebra (trigonometria) (Azonosító: mmk_201310_1r03f )

Oldja meg a $[-\pi; \pi]$ zárt intervallumon a $\cos x =\dfrac{1}{2}$ egyenletet!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

4. találat: Matematika középszintű érettségi, 2013. október, I. rész, 4. feladat
Témakör: *Számelmélet (logika, LNKO) (Azonosító: mmk_201310_1r04f )

Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)!

A) Két különböző pozitív egész szám legnagyobb közös osztója mindig kisebb mindkét számnál.

B) Két különböző pozitív egész szám legnagyobb közös osztója mindig osztója a két szám összegének.

C) Két különböző pozitív egész szám legnagyobb közös osztója nem lehet 1.

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

5. találat: Matematika középszintű érettségi, 2013. október, I. rész, 5. feladat
Témakör: *Algebra (szöveges egyenlet, százalék) (Azonosító: mmk_201310_1r05f )

Egy országban egy választáson a szavazókorú népesség 63,5%-a vett részt. A győztes pártra a résztvevők 43,6%-a szavazott. Hány fős a szavazókorú népesség, ha a győztes pártra 4 152 900 fő szavazott? Válaszát indokolja!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

6. találat: Matematika középszintű érettségi, 2013. október, I. rész, 6. feladat
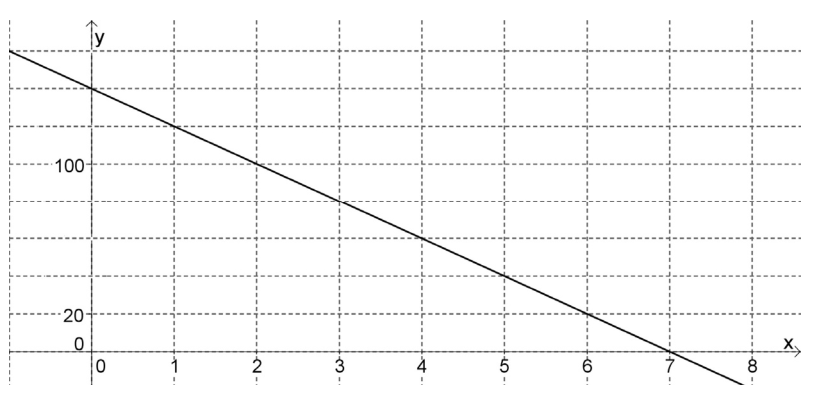
Témakör: *Függvények (lineáris, egyenes) (Azonosító: mmk_201310_1r06f )

Megoldás:

b = 140; m = -20

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

7. találat: Matematika középszintű érettségi, 2013. október, I. rész, 7. feladat
Témakör: *Geometria (egybevágóság) (Azonosító: mmk_201310_1r07f )

Adja meg, hogy az alábbi geometriai transzformációk közül melyek viszik át önmagába az ábrán látható, háromszög alakú (sugárveszélyt jelző) táblát!

A) 60°-os elforgatás a tábla középpontja körül.

B) 120°-os elforgatás a tábla középpontja körül.

C) Középpontos tükrözés a tábla középpontjára.

D) Tengelyes tükrözés a tábla középpontján és a tábla egyik csúcsán átmenő tengelyre.

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

8. találat: Matematika középszintű érettségi, 2013. október, I. rész, 8. feladat
Témakör: *Sorozatok (algebra, egyenletrendszer, lineáris) (Azonosító: mmk_201310_1r08f )

Egy számtani sorozat hatodik tagja 15, kilencedik tagja 0. Számítsa ki a sorozat első tagját! Válaszát indokolja!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

9. találat: Matematika középszintű érettségi, 2013. október, I. rész, 9. feladat
Témakör: *Kombinatorika (gráf) (Azonosító: mmk_201310_1r09f )

Rajzoljon egy olyan 5 csúcsú gráfot, melyben a csúcsok fokszámának összege 12.

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

10. találat: Matematika középszintű érettségi, 2013. október, I. rész, 10. feladat
Témakör: *Függvények (exponenciális) (Azonosító: mmk_201310_1r10f )

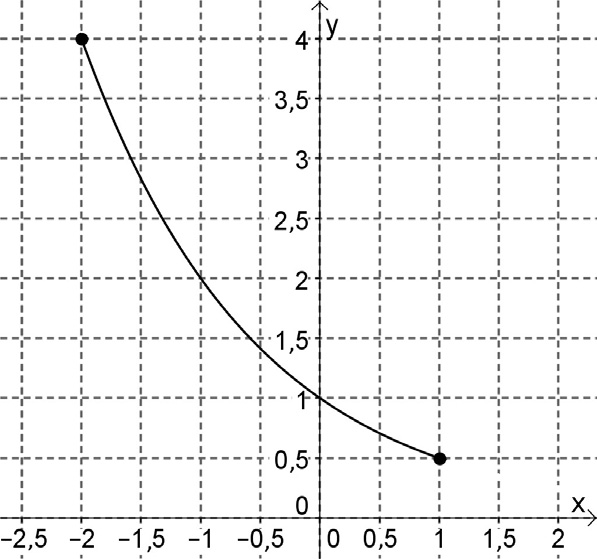
Az ábrán az $f:[-2;1]\rightarrow \mathbb{R}; f(x)=a^x$ függvény grafikonja látható.

a) Adja meg az f függvény értékkészletét! b) Határozza meg az a szám értékét!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

11. találat: Matematika középszintű érettségi, 2013. október, I. rész, 11. feladat
Témakör: *Valószínűségszámítás (számelmélet, osztó) (Azonosító: mmk_201310_1r11f )

Adja meg annak az eseménynek a valószínűségét, hogy egy szabályos dobókockával egyszer dobva a dobott szám osztója a 60-nak! Válaszát indokolja!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

12. találat: Matematika középszintű érettségi, 2013. október, I. rész, 12. feladat
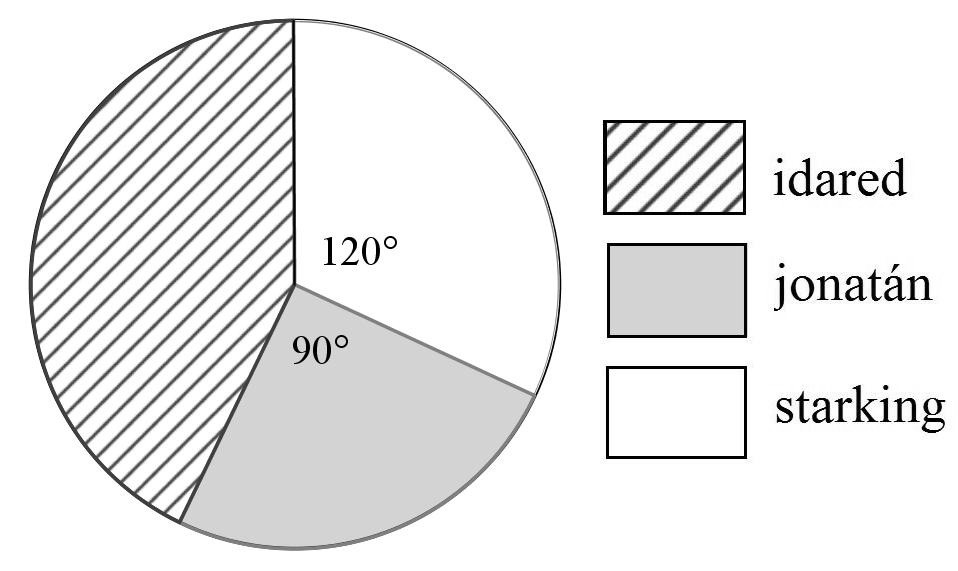
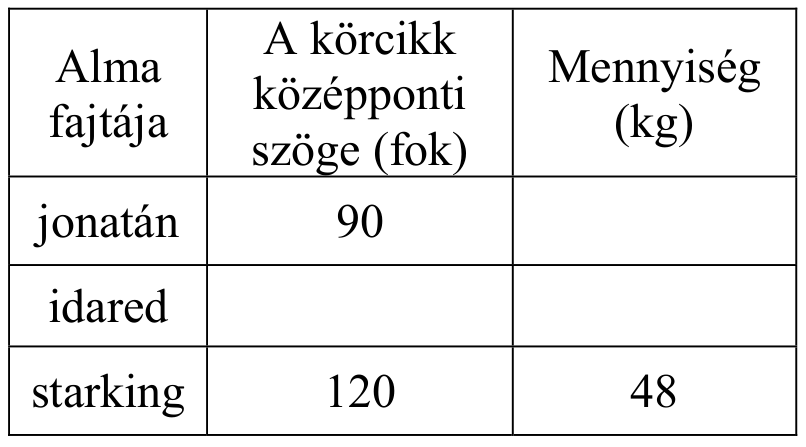
Témakör: *Algebra (arány, körcikk) (Azonosító: mmk_201310_1r12f )

Egy gyümölcsárus háromféle almát kínál a piacon. A teljes készletről kördiagramot készítettünk. Írja a táblázat megfelelő mezőibe a hiányzó adatokat!