Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
10 720 703 Mai:
3 128 18-97-14-88.crawl.commoncrawl.org
(IP: 18.97.14.88) HonlapokSULINET Matematika Oktatási Hivatal Versenyvizsga portál Matematika Portálok |
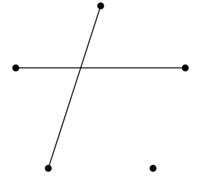
1. találat: Matematika középszintű érettségi, 2016. október, I. rész, 1. feladat Témakör: *Kombinatorika (gráf) (Azonosító: mmk_201610_1r01f ) Az ábrán látható ötpontú gráfot egészítse ki további élekkel úgy, hogy mindegyik pont fokszáma 2 legyen!
Témakör: *Függvények (függvény) (Azonosító: mmk_201610_1r02f ) Melyik számot rendeli az $x \mapsto \sqrt[3]{4x-1};\quad(x\in \mathbb{R})$ függvény a 7-hez? Témakör: *Számelmélet (prím, prímszám) (Azonosító: mmk_201610_1r03f ) Írja fel a 38-at két különböző prímszám összegeként! Témakör: *Kombinatorika (permutáció) (Azonosító: mmk_201610_1r04f ) Hány olyan négyjegyű pozitív egész szám van a tízes számrendszerben, amelynek négy különböző páratlan számjegye van? Témakör: *Koordinátageometria (logika, egyenes, felezőpont, párhuzamos) (Azonosító: mmk_201610_1r05f ) Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)! A: Az (1; –1) pont rajta van az 5x – 3y = 2 egyenletű egyenesen. B: Ha A(–2; 5) és B(2; –3), akkor az AB szakasz felezőpontja a (0; 2) pont. C: Az x + 2y = 7 és a 2x + 4y = 7 egyenletű egyenesek párhuzamosak. Témakör: *Térgeometria (térfogat, henger) (Azonosító: mmk_201610_1r06f ) A diákok az egyik kémiaórán két mérőhengert használnak. Az egyik henger magassága és alapkörének átmérője is feleakkora, mint a másiké. Hányszorosa a nagyobb mérőhenger térfogata a kisebb mérőhenger térfogatának? Válaszát indokolja! 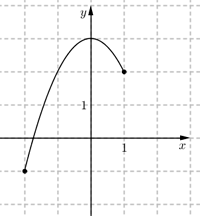Témakör: *Függvények (értékkészlet, parabola, másodfokú) (Azonosító: mmk_201610_1r07f ) Adja meg az alábbi ábrán látható, a [–2; 1] intervallumon értelmezett $x \mapsto -x^2 +3$ függvény értékkészletét!
Témakör: *Trigonometria (sinus) (Azonosító: mmk_201610_1r08f ) Adja meg a $\sin x = \dfrac{1}{2}$ egyenlet $\pi$-nél kisebb, pozitív valós megoldásait! Témakör: *Algebra (százalék, szöveges feladat) (Azonosító: mmk_201610_1r09f ) Egy kirándulócsoport 8 km-es túrára indult. Már megtették a 8 km 40%-át és még 1200 métert. A tervezett út hány százaléka van még hátra? Számításait részletezze! Témakör: *Algebra (log, logaritmus, azonosság) (Azonosító: mmk_201610_1r10f ) Adja meg a következő összeg értékét: $\log_6 2 + \log_6 3$ . Témakör: *Függvények (zérushely, abszolútérték) (Azonosító: mmk_201610_1r11f ) Adja meg a valós számok halmazán értelmezett f függvény zérushelyeit, ha $f(x)=\left | x-1 \right |-3$ . Válaszát indokolja! Témakör: *Valószínűségszámítás (dobókocka) (Azonosító: mmk_201610_1r12f ) Szabályos dobókockával négyszer dobunk egymás után. A dobott számokat sorban egymás mellé írjuk. Tekintsük az alábbi dobássorozatokat: a) 5, 1, 2, 5; b) 1, 2, 3, 4; $\qquad$c) 6, 6, 6, 6. Válassza ki az alábbi állítások közül azt, amelyik igaz: A) Az a) dobássorozat bekövetkezése a legvalószínűbb a három közül. B) A b) dobássorozat bekövetkezése a legvalószínűbb a három közül. C) A c) dobássorozat bekövetkezése a legvalószínűbb a három közül. D) Mindhárom dobássorozat bekövetkezésének ugyanannyi a valószínűsége.
|
KeresésHonlapokKözépiskolai Matematikai és Fizikai Lapok Wolfram Alpha Art of Problem Solving Kvant IMO |
|||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
| |||||||||||||||||||
| |||||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
|
1082 Budapest, Horváth Mihály tér 8. OM azonosító: 035277 |
Joomla template: szsnjm4-001 (c) Szoldatics József 2011/2025
www.szolda.hu
www.szolda.hu