| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
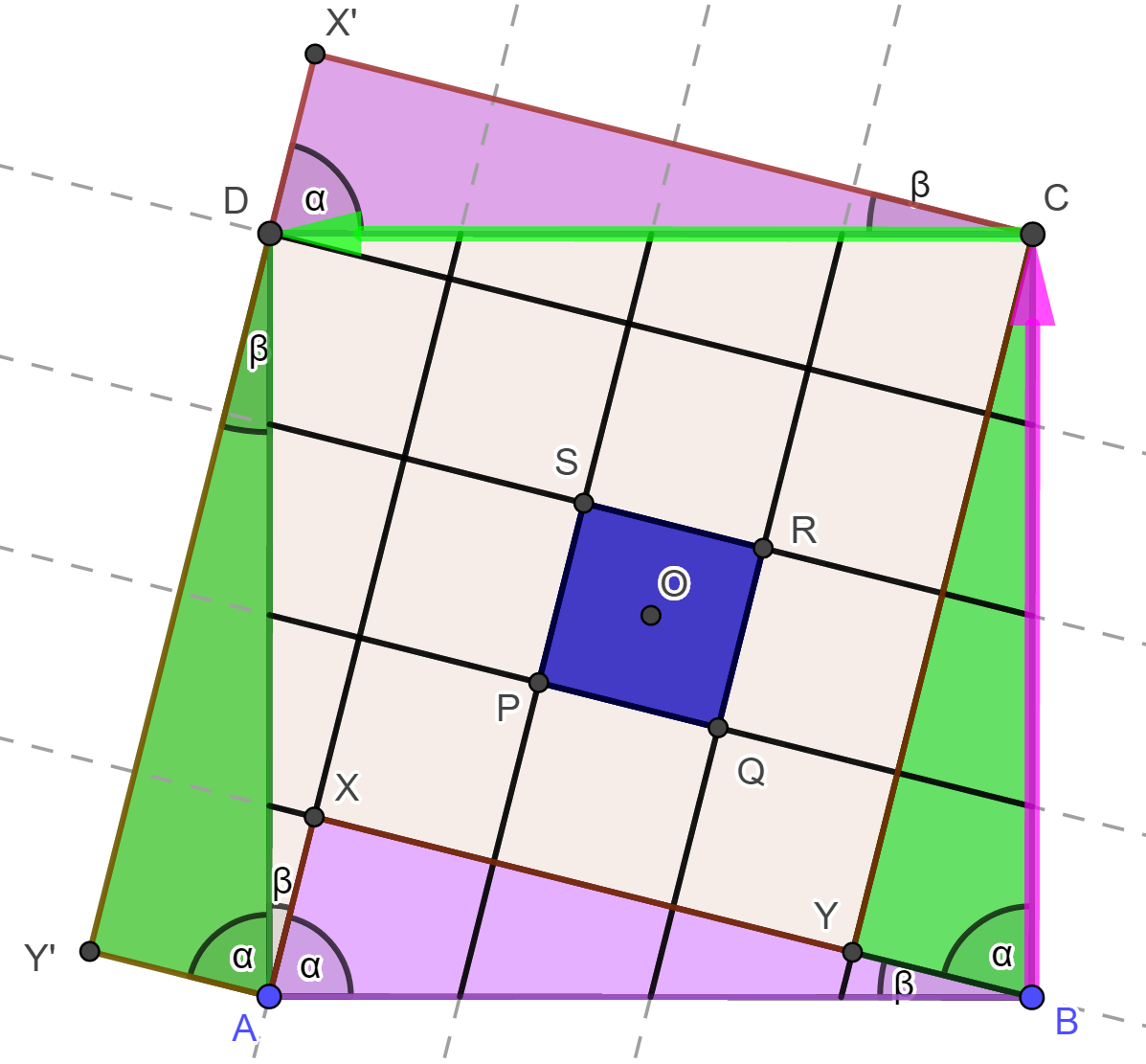
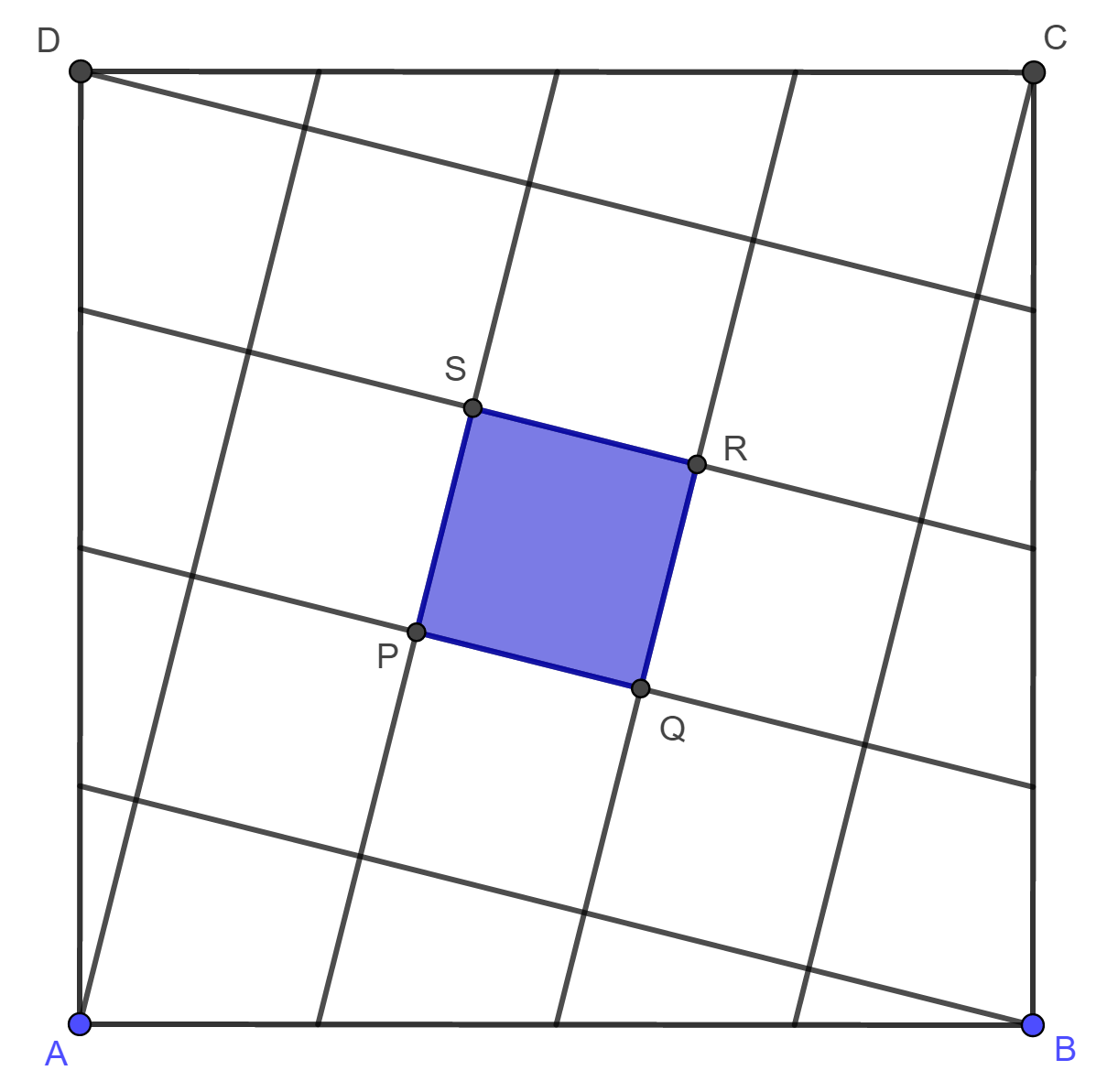
| Az ABCD négyzet minden oldalát 4 egyenlő részre osztjuk, majd az ábra szerinti osztópontokat összekötjük. Milyen négyszög a PQRS négyszög? Hányadrésze a PQRS négyszög területe az ABCD négyzet területének? |
| Vizsgáljuk
meg a Forgatás nevű
csúszka segítségével a PQRS
négyszög szimmetria-tulajdonságait! Milyen
következtetések vonhatók le ebből a PQRS négyszögre? Az 1.eltolás, majd a 2.eltolás nevű csúszkák segítségével határozzuk meg a két négyszög területének arányát!
A Forgatás csúszka animálása mellett megfigyelhetjük, hogy az ABCD négyzet szemközti oldalait (pl. az AB és CD oldalt) összekötő szakaszokat az ABCD négyzet O középpontja körüli 90°-os forgatás a másik két szemközti oldalt (BC és AD) összekötő megfelelő szakaszokba viszi át. Ebből következik, hogy az ábra (és így persze a PQRS négyszög is) forgásszimmetrikus az O pont körüli 90°-os, 180°-os, 270°-os forgatásokra nézve. Egyetlen ilyen tulajdonságú négyszög van, mégpedig a négyzet, ezért a PQRS négyszög négyzet, melynek középpontja az O pont. Most
vizsgáljuk meg a PQRS
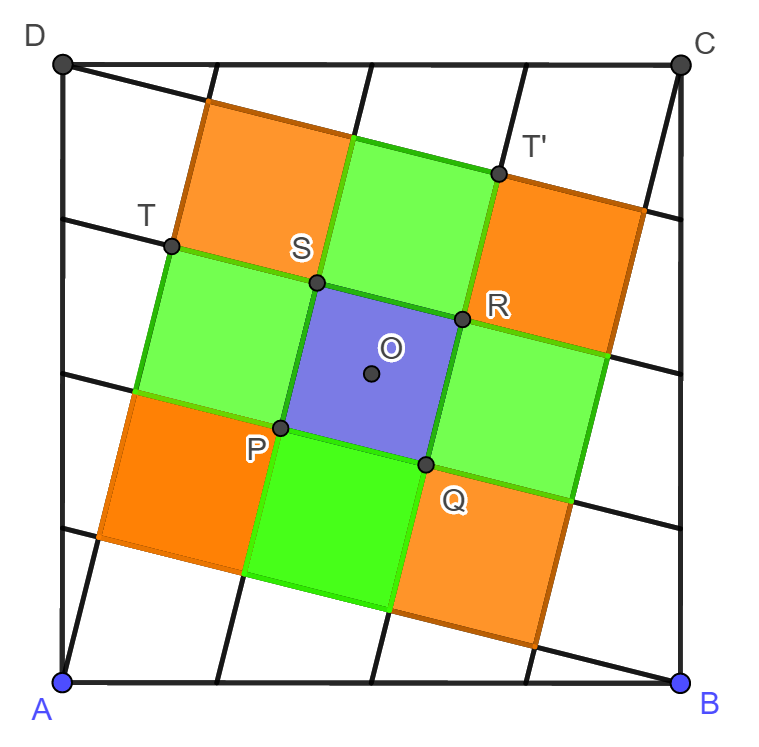
négyszöghöz csatlakozó négyszögeket! Az alábbi animáció mutatja (és
könnyen végig is gondolható), hogy az azonos színnel megjelölt
négyszögek 90°-os, 180°-os vagy 270°-os forgatással egymásba vihetők,
ezért egybevágók egymással. Mivel a (legkisebb szögű) forgatás szöge
90°, ezért a színes négyszögek mindegyikében merőlegesek a
szomszédos oldalak, azaz mind téglalap. Az O pont körüli
90°-os forgatás a T
pontot T’-be,
S-et
R-be
viszi át, ezért TS=T’R,
amiből már következik, hogy a narancssárga téglalapok szomszédos
oldalai egyenlők, így mindegyik négyzet. Ekkor viszont a zöld
téglalapok is négyzetek, végül láthatjuk, hogy az ábra összes színessel
megjelölt négyzete egybevágó egymással.
A
következő animációban az ABX
és BCY
derékszögű háromszögek eltolását figyelhetjük meg. Toljuk el az ABX háromszöget
a
Az
átdarabolást eltolás helyett forgatással is elvégezhetjük a feladat
2. megoldásában. |
 , a
, a 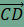 vektorral. Ha
vektorral. Ha 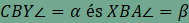
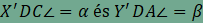 , ezért a
, ezért a 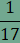 .
.