Árki Tamás és Hraskó András
Kísérletező geometria
Készült a Közoktatási Modernizációs Közalapítvány (KOMA) támogatásával
Hraskó András
Morley tétele
Ez volt a gondolatmenet. A bizonyítás már egy sokkal egyszerűbb dolog. Frank Morley
|
|
morleyproof_a. ábra.
|
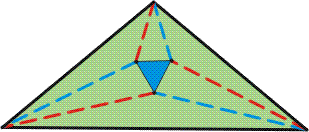
Alább az elemi(?) geometria egy viszonylag új, különleges tételét fogalmazzuk meg:
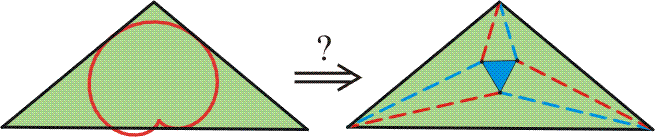
Morley 1906 körül fedezte fel a tételt. Elmesélte barátainak, akik elterjesztették és hamar sokan, sokféle bizonyítást adtak rá. Néhány szép bizonyítás magyar nyelven is elérhető, lásd a cikk végén található irodalomjegyzéket. Jóval a felfedezés után, 1920-ban, Morley megírta egy japán ismerősének, T. Hayashi professzornak, a tétel felfedezésének történetét, amit a professzor leközölt egy japán lapban. E levél alapján, és az azóta ahhoz készített kommentárokat felhasználva próbáljuk bemutatni az utat, amelyen Morley eljutott a háromszög oldalait érintő kardioidok rendszerétől a szabályos háromszögig.
|
|
morleyproof_b. ábra.
|

|
|
|
morleyproof_c. ábra.
|
morleyproof_d. ábra.
|
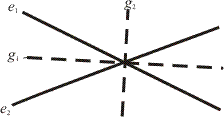
Körhöz külső pontból két érintő húzható. Ha valamely pontból egy körhöz meghúzzuk a két érintőt, akkor a kör középpontja rajta lesz a két érintő alkotta szög szögfelező egyenesén (morleyproof_c. ábra).
Legyen most adva két egyenes (a morleyproof_d. ábrán e1 és e2). Kereshetjük azokat a köröket, amelyek mind a két egyenest érintik. Nem nehéz meggondolni, hogy az ilyen körök középpontjának mértani helye a két adott egyenes két szögfelező egyenese, két egymásra merőleges egyenes (a morleyproof_d. ábrán g1 és g2).

|
|
|
morleyproof_e. ábra.
|
morleyproof_f. ábra.
|
A kardioid görbe a körhöz hasonló tulajdonságú. Erről szól Morley alábbi észrevétele.
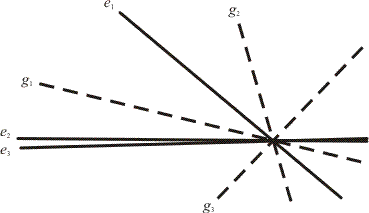
b) Ha valamely pontból egy kardioidhoz meghúzzuk a három érintőt, akkor a kardioid centruma rajta lesz az érintők egyik szögharmadoló egyenesén (morleyproof_e. ábra).
c) Legyen adva három egy ponton átmenő egyenes (a morleyproof_f. ábrán e1, e2) és e3). Azon kardioidok centrumának mértani helye, amelyek mind a három egyenest érintik, a három egyenes három szögharmadoló egyenese, három egymással 60°-os szöget bezáró egyenes (a morleyproof_f. ábrán g1, g2 és g3).
Ha adott három egy pontól induló egyenes, akkor szögharmadolóikat a következőképpen értelmezhetjük. Vegyünk fel egy tetszőleges irányt, mérjük le ehhez képest az egyenesek szögét, adjuk össze a három értéket, és osszuk le hárommal. Az így kapott szöget mérjük fel az előbb tetszőlegesen választott irányhoz képest.
A hárommal való osztásnak háromféle értéke van mod 360°, amelyek egymástól 120°-kal térnek el. Valóban, a hárommal való szorzás azonossá teszi az egymástól eredetileg 120° egész számú többszörösével eltérő értékeket. Ezért van három szögharmadoló.
A szögharmadoló egyenesek nem függenek származtatásuk elején tetszőlegesen választott iránytól. Valóban, ha ezt az irányt α szöggel módosítjuk, akkor az adott egyeneseknél mért érték -α szöggel (vagy ehhez képest még ±180°-kal), a szögösszeg -3α szöggel (+k·180°, ahol k egész), a harmad értéke -α-val (+k·60°) változik, így a szögharmadolók ugyanazok az egyenesek maradnak.
Háromszögbe írt körök és duplán érintő kardioidok
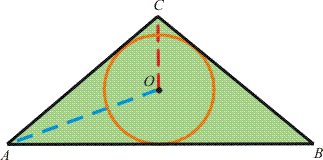
Ha egy háromszög mindhárom oldalegyenese érint egy kört, akkor a kör középpontja rajta van a háromszög szögfelezőinek metszéspontján (lásd a morleyproof_g. ábrát).
|
|
morleyproof_g. ábra.
|
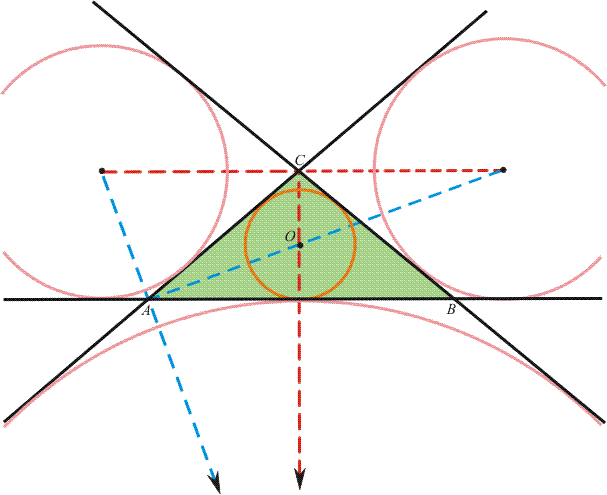
Ha meg akarjuk találni a háromszög mindhárom oldalegyenesét érintő összes kört, akkor elég két csúcsnál berajzolni a szögfelezőket. Mivel mindkét csúcsnál két szögfelezőt találunk, így négy metszéspont jön létre, négy megfelelő kör van (lásd a morleyproof_h. ábrát).
|
|
morleyproof_h. ábra.
|
Morley vizsgálta a háromszög mindhárom oldalát érintő kardioidok rendszerét. Ilyen kardioidból végtelen sok van, centrumuk mértani helyének meghatározására később, Morley III. állításával, még visszatérünk.
A kardioid abban is különbözik a körtől, hogy lehet, hozzá olyan érintőt is húzni, amely két helyen is, tehát kétszeresen érinti a görbét. Olyan kardioidból, amely egy adott háromszög mindhárom oldalegyenesét érinti, az egyiket kétszeresen is, már csak véges sok van.
|
|
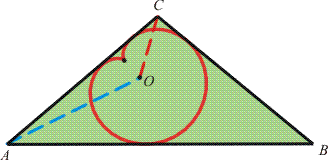
morleyproof_i. ábra.
|
Alkalmazzuk Morley I. Állítását! Az A pontból a kardioidhoz húzható három érintő: AB, AC és megint AC. Morley első állítása szerint a kardioid centruma illeszkedik e három érintő szögharmadolójára, azaz a BAC∠ szög AC felőli szögharmadolójára.
Hasonló okból a kardioid centruma a BCA∠ szög AC felőli szögharmadolójára is illeszkedik, tehát ezek metszéspontjában van.
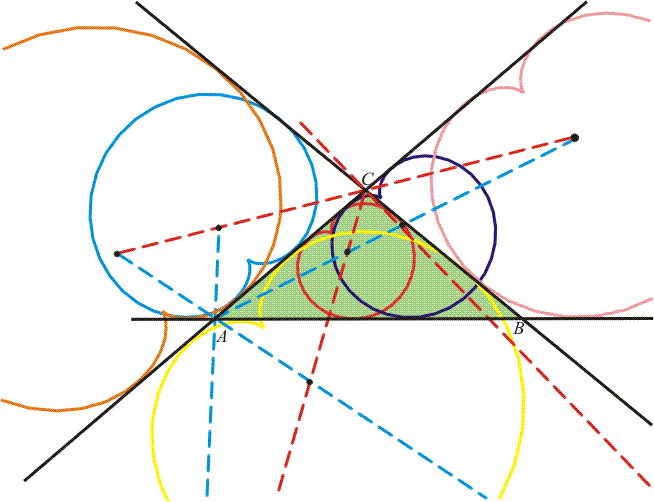
|
|
morleyproof_j. ábra.
|
A háromszögbe írt összes kardioid
Az indoklás bizonyára kivitelezhető lenne az egyeneseknek az szv00702 feladatban szereplő konkrét egyenletei révén, az addíciós tételek alkalmazásával. De Morley nem így gondolkodott. Próbáljuk meg követni az Ő gondolatmenetét! Alább már feltételezzük, hogy a centrumok egyeneseken helyezkednek el, itt csak az egyenesek állását diszkutáljuk.
Képzeljük el háromszögünket és egy annak oldalait érintő nagyon távoli centrumú kardioidot. Az a kérdés, hogy ez a centrum milyen irányban lehet a háromszögtől. Ha messzorőlnézünk erre az ábrára, akkor háromszögünk alig lesz megkülönböztethető egyetlen ponttól. Mintha egyetlen pontból húztuk volna meg a három érintőt ugyanahhoz a kardioidhoz.
Morley I. állításának b) része szerint a kardioid centrumának az oldalegyenesek irányai átlagának irányában kell elhelyezkednie minden ilyen nagy kardioidra. Tehát a kardioidok centrumait tartalmazó egyenesek párhuzamosak a háromszög oldalegyenes-irányainak három szögharmadolójával.
A szögharmadolók egymással 60°- ill. 120°-os szöget zárnak be, így az állítást beláttuk.
Morley tétele, mint nem várt ajándék
A háromszög oldalegyeneseit érintő kardioidok vizsgálata közben, mintegy véletlenül futott össze Morley a később híressé vált tétellel.

|
|
morleyproof_k. ábra. A kép
|