Látogatók
Összes: 6 065 942 Mai: 1 438
|
1. találat: Matematika emelt szintű érettségi, 2020. október, II. rész, 5. feladat
Témakör: *Algebra (Azonosító: mme_202010_2r05f )
Adott négy, a valós számok halmazán értelmezett függvény: $ f(x) = (x + 4)(2 - x);\qquad g(x) = x + 4 $ $ h(x) = x^2 - 4;\qquad (x) = \left| x \right| - 4 $ a) Határozza meg az $ f $ és $ g $ függvények grafikonja által közrezárt korlátos síkidom területét!
Egy négypontú gráf csúcsait megfeleltetjük e négy függvénynek. Két csúcsot pontosan akkor kötünk össze éllel, ha a két megfelelő függvénynek van közös zérushelye.
b) Rajzolja fel az így kapott gráfot!
A valós számok halmazán értelmezett $ k $ függvény zérushelyei $ -5 $ és $ 3 $, az $ m $ függvény zérushelyei $ 3 $ és $ -3 $, az $ n $ függvény zérushelyei pedig $ 5 $ és $ -5 $. A $ p $ elsőfokú függvény hozzárendelési szabálya $ p(x) = x + c $, ahol $ c $ egy valós szám.
c) Hányféleképpen választható meg a $ c $ konstans értéke úgy, hogy a $ k $, $ m $, $ n $ és $ p $ függvényekre a b) feladatban megadott szabály szerint elkészített négypontú gráf fagráf legyen?
*Algebra (Azonosító: mme_202010_2r06f )
Egyes kutatók szerint a városokban az influenzával fertőzött betegek száma a $ B(t)=\dfrac{L}{1+\left( \dfrac{L}{B_0}-1\right)\cdot 0,75^t} $ formula szerint alakul. A képletben t az influenzajárvány kezdetétől eltelt idő napokban kifejezve $ (0 \le t < 30) $, L a város lakosainak száma, B0 pedig a járvány kezdetekor a fertőzött betegek száma a városban $(0 < B_0 < L) $. Egy nagyvárosban L = 1,5 millió, $B_0$ = 1000.
a)A modell szerint hány fertőzött betegre lehet számítani ebben a városban a járvány kezdete után 5 nappal?
b) Hány nap múlva lesz a város lakosainak 10%-a fertőzött beteg a modell szerint?
c) Igazolja, hogy ha $ L $ és $ K $ adott pozitív számok, $ n \in \mathbb{N}^+ $, akkor a $ b_n = \dfrac{L}{1 + K \cdot 0,75^n} $ képlettel megadott sorozat korlátos, szigorúan monoton növekedő, és $ \lim\limits_{n\to\infty} b_n = L $.
*Geometria (Azonosító: mme_202010_2r07f )
Ádám balatoni telkén áll egy kis hétvégi ház. A ház felülnézete egy 7 m × 4 m-es téglalap. Ha esik az eső, akkor a tetőre lehulló csapadékot a tető négy oldalán körbefutó ereszcsatornák gyűjtik össze és vezetik be négy nagy, kezdetben üres (fedett) hordóba. A hordók forgáshenger alakúak, belső átmérőjük 40 cm, magasságuk 90 cm. Egy nyári zivatar alkalmával 15 mm csapadék hullott a településen (ez azt jelenti, hogy minden vízszintes felületen 15 mm magasan állna az esővíz, ha nem szivárogna el). A zivatar közben a tetőre lehullott csapadék 95%-a összegyűlt a hordókban.
a) A zivatar után mindegyik hordóban ugyanolyan magasan állt a víz. Mekkora ez a magasság?
A ház cserépteteje elöregedett, cserélni kell. A tető felülete négy síkidomból áll. A háztető 7 méteres oldalaihoz két egybevágó húrtrapéz csatlakozik, amelyek síkja a vízszintessel egyaránt 30 fokos szöget zár be. A trapézok egymáshoz csatlakozó, rövidebb oldala 3 méter hosszú. A háztető 4 méteres oldalaihoz két egybevágó, egyenlő szárú háromszög csatlakozik. 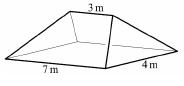 b) Hány darab cserepet kell vásárolnia Ádámnak a tető újracserepezéséhez, ha a tetőfelület egy négyzetméterére 30 darabra van szükség, és a megvásárolt mennyiség 8%-a hulladék lesz? b) Hány darab cserepet kell vásárolnia Ádámnak a tető újracserepezéséhez, ha a tetőfelület egy négyzetméterére 30 darabra van szükség, és a megvásárolt mennyiség 8%-a hulladék lesz?
*Kombinatorika (Azonosító: mme_202010_2r08f )
Legyen az alaphalmaz a háromjegyű pozitív egész számok halmaza. Az A halmaz elemei azok a háromjegyű számok, amelyekben van 1-es, a B halmaz elemei azok, amelyekben van 2-es, a C halmaz elemei pedig azok, amelyekben van 3-as számjegy.
a) Hány eleme van az $ A \setminus (B \cap C) $ halmaznak?
Egy szerepjátékhoz használt dobókocka három lapján 3-as, két lapján 2-es, egy lapján 1-es szám van. A feldobott kocka mindegyik lapjára egyforma valószínűséggel esik.
b) Két ilyen dobókockával egyszerre dobva mennyi a valószínűsége annak, hogy a dobott számok összege 4 lesz?
Andi és Béla a következő játékot játsszák ezzel a dobókockával. Valamelyikük dob egyet a kockával. Ha a dobás eredménye 3, akkor Andi fizet Bélának n forintot (n > 80); ha a dobás eredménye 1, akkor Béla fizet (n – 80) forintot Andinak; ha pedig a dobás eredménye 2, akkor is Béla fizet Andinak 2(n – 80) forintot.
c) Mennyit fizet Béla Andinak az 1-es dobása esetén, ha ez a játék igazságos, azaz mindkét játékos nyereményének várható értéke 0?
*Kombinatorika (Azonosító: mme_202010_2r09f )
Az $ ABC $ szabályos háromszög mindhárom oldalát 3-3 osztóponttal négy egyenlő részre osztottuk. 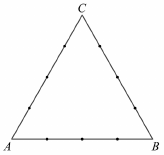 a) Hány olyan négyszög van, melynek mind a négy csúcsa a háromszög oldalain kijelölt 9 pont közül való úgy, a) Hány olyan négyszög van, melynek mind a négy csúcsa a háromszög oldalain kijelölt 9 pont közül való úgy,
hogy a négyszögnek a háromszög mindegyik oldalán van legalább egy csúcsa? (Két négyszöget különbözőnek tekintünk, ha legalább egy csúcsukban különböznek.)
Jelölje a 4 egység oldalú $ ABC $ szabályos háromszög $ BC $ ol dalának $ B $-hez közelebbi negyedelőpontját $ P $, a $ CA $ oldal $ C $-hez közelebbi negyedelőpontját $ Q $, az $ AB $ oldal $ A $-hoz közelebbi negyedelőpontját pedig $ R $. Jelölje továbbá $ AP $ és $ BQ $ szakaszok metszéspontját $ X $, $ BQ $ és $ CR $ szakaszok metszéspontját $ Y $, végül $ CR $ és $ AP $ szakaszok metszéspontját $ Z $.
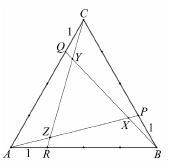
b) Határozza meg az $ XYZ $ vháromszög területét!
|
|


