Egy háromszög csúcsainak koordinátái: A(–2; –1), B(9; –3) és C(–3; 6).

a) Írja fel a BC oldal egyenesének egyenletét!

b) Számítsa ki a BC oldallal párhuzamos középvonal hosszát!

c) Számítsa ki a háromszögben a C csúcsnál lévő belső szög nagyságát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

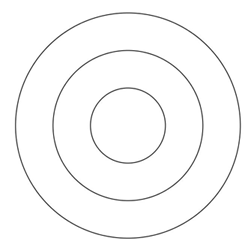
Egy ajándéktárgyak készítésével foglalkozó kisiparos családi vállalkozása keretében zászlókat, kitűzőket is gyárt. Az ábrán az egyik általa készített kitűző stilizált képe látható. A kitűzőn lévő három mező kiszínezéséhez 5 szín (piros, kék, fehér, sárga, zöld) közül választhat. Egy mező kiszínezéséhez egy színt használ, és a különböző mezők lehetnek azonos színűek is.

a) Hányféle háromszínű kitűzőt készíthet a kisiparos?

b) Hányféle kétszínű kitűző készíthető?

A kisiparos elkészíti az összes lehetséges különböző (egy-, két- és háromszínű) kitűzőt egy-egy példányban, és véletlenszerűen kiválaszt közülük egyet.

c) Mennyi annak a valószínűsége, hogy olyan kitűzőt választ, amelyen az egyik mező kék, egy másik sárga, a harmadik pedig zöld színű?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyenek f és g a valós számok halmazán értelmezett függvények, továbbá:

$f(x)=5x+5,25$  és  $g(x)=x^2+2x+3,5$

a) Számítsa ki az alábbi táblázatok hiányzó értékeit!

b) Adja meg a g függvény értékkészletét!
c) Oldja meg az $ 5x+5,25 > x^2+2x+3,5$ egyenlőtlenséget a valós számok halmazán!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Stefi mobiltelefon-költségeinek fedezésére feltöltőkártyát szokott vásárolni. A mobiltársaság ebben az esetben sem előfizetési díjat, sem hívásonkénti kapcsolási díjat nem számol fel. Csúcsidőben a percdíj 25 forinttal drágább, mint csúcsidőn kívül. Stefi az elmúlt négy hétben összesen 2 órát telefonált és 4000 Ft-ot használt fel kártyája egyenlegéből úgy, hogy ugyanannyi pénzt költött csúcsidőn belüli, mint csúcsidőn kívüli beszélgetésekre.

a) Hány percet beszélt Stefi mobiltelefonján csúcsidőben az elmúlt négy hétben?

A mobiltársaság Telint néven új mobilinternet csomagot vezet be a piacra január elsején. Januárban 10000 új előfizetőt várnak, majd ezután minden hónapban az előző havinál 7,5%-kal több új előfizetőre számítanak. Abban a hónapban, amikor az adott havi új előfizetők száma eléri a 20000-et, a társaság változtatni szeretne a Telint csomag árán.

b) Számítsa ki, hogy a tervek alapján melyik hónapban éri el a Telint csomag egyhavi új előfizetőinek a száma a 20000-et!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy szabályos négyoldalú (négyzet alapú) gúla alapéle 12 cm, oldallapjai $ 60^{\circ}$-os szöget zárnak be az alaplap síkjával.

a) Számítsa ki a gúla felszínét ($cm^2$-ben) és térfogatát ($cm^3$-ben)! Válaszait egészre kerekítve adja meg!

A gúlát két részre osztjuk egy az alaplappal párhuzamos síkkal, amely a gúla magasságát a csúcstól távolabbi harmadoló pontban metszi.

b) Mekkora a keletkező gúla és csonkagúla térfogatának aránya? Válaszát egész számok hányadosaként adja meg!

c) Számítsa ki a keletkező csonkagúla felszínét $cm^2$-ben!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az egyik világbajnokságon részt vevő magyar női vízilabdacsapat 13 tagjának életkor szerinti megoszlását mutatja az alábbi táblázat.

a) Számítsa ki a csapat átlagéletkorát!

Jelölje A azt az eseményt, hogy a csapatból 7 játékost véletlenszerűen kiválasztva, a kiválasztottak között legfeljebb egy olyan van, aki 20 évnél fiatalabb.

b) Számítsa ki az A esemény valószínűségét! A világbajnokság egyik mérkőzésén a magyar kezdőcsapat 6 mezőnyjátékosáról a következőket tudjuk:

• a legidősebb és a legfiatalabb játékos életkorának különbsége 12 év,

• a játékosok életkorának egyetlen módusza 22 év,

• a hat játékos életkorának mediánja 23 év,

• a hat játékos életkorának átlaga 24 év.

c) Adja meg a kezdőcsapat hat mezőnyjátékosának életkorát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba