a) Oldja meg az alábbi egyenletet a valós számok halmazán!

$ (2x-3)^2=x^2$

b) Hány olyan (pozitív) háromjegyű páratlan szám van a tízes számrendszerben, amelynek minden számjegye különböző?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 30 fős osztály matematikaérettségi vizsgájának érdemjegyei olvashatók le az alábbi diagramról.

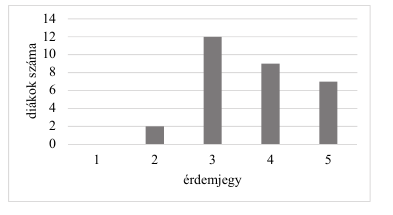
a)Adja meg az osztály matematikaérettségi érdemjegyeinek átlagát, mediánját és móduszát!

b) Ábrázolja az érdemjegyek eloszlását kördiagramon!

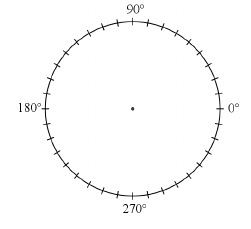
Az osztály tanulóinak matematikaérettségi dolgozatai közül az érettségi elnök véletlenszerűen kiválaszt és megvizsgál kettőt.

c) Számítsa ki annak a valószínűségét, hogy mindkét kiválasztott dolgozat érdemjegye hármas! Válaszát három tizedesjegyre kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Két derékszögű háromszöget egy-egy oldalukkal egymáshoz illesztettünk az ábrának megfelelően.Így az ABCD derékszögű trapézt kaptuk.

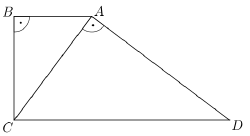
a) Igazolja, hogy az ABC és a CAD háromszög hasonló!

Legyen AB = 9 cm, AC = 15 cm.

b) Számítsa ki a trapéz AD oldalán fekvő szögeinek nagyságát!

c) Számítsa ki a trapéz területét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A mobiltelefonok 1990 végén jelentek meg Magyarországon. Az előfizetések száma gyorsan nőtt: 2002 végén már kb. 7 millió, 2008 végén pedig kb. 12 millió előfizetés volt az országban.

a) Hány százalékkal nőtt a mobiltelefon előfizetések száma 2002 végétől 2008 végéig?

1993 és 2001 között az egyes évek végén nyilvántartott mobiltelefon-előfizetések számát – ezer darabban – jó közelítéssel a következő függvény adja meg: $ f ( x)=51\cdot 1,667^x $ , ahol x az 1992 vége óta eltelt évek számát jelöli.

b) A függvény alapján hány mobiltelefon-előfizető lehetett 2000 végén?

A kezdeti időszakban a mobilhálózatból indított hívások száma is gyors növekedést mutatott. 1991 januárjában Magyarországon körülbelül 350 000 mobilhívást indítottak, majd ettől a hónaptól kezdve minden hónapban megközelítőleg 6,5%-kal nőtt a hívások száma az előző havi hívások számához viszonyítva (egészen 2002-ig).

c)Melyik évben volt az a hónap, amelyben az egy havi mobilhívások száma először elérte a 100 milliót?

A mobiltelefonok elterjedése egy idő után a vezetékestelefon-előfizetések és hívások szá mának csökkenését eredményezte. A vezetékestelefon-hálózatból indított hívások száma Magyarországon 2000-ben kb. 4200 millió volt, majd ez a szám évről évre kb. 8%-kal csökkent.

d) Hány hívást indítottak vezetékes hálózatból 2009-ben, és összesen hány vezetékes hívás volt a 2000 elejétől 2009 végéig terjedő tízéves időszakban?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A derékszögű koordináta-rendszerben adott a $ 4x + y = 17 $ egyenletű e egyenes, továbbá az e egyenesre illeszkedő $ C(2; 9) $ és $ T(4; 1) $ pont. Az A pont az origóban van.

a) Igazolja, hogy az ATC szög derékszög!

Az A pont e egyenesre vonatkozó tükörképe a B pont.

b) Számítsa ki a B pont koordinátáit!

c) Határozza meg az ABC egyenlő szárú háromszög körülírt köre középpontjának koordinátáit!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy matematikaversenyen 25 feladatot kell a résztvevőknek megoldaniuk 75 perc alatt. A felkészülés során Vera azt tervezgeti, hogy mennyi időt töltsön majd a könnyebb feladatok megoldásával, és mennyi időt hagyjon a nehezebbekre. Az első feladatra 1 percet szán. A versenyfeladatok általában egyre nehezedő sorrendben vannak megadva; Vera ezt úgy veszi figyelembe a tervezésnél, hogy a második feladattól kezdve mindig ugyanannyival növeli az egyes feladatok megoldására fordítható időt. Vera a rendelkezésére álló teljes időtartamot szeretné kitölteni a feladatok megoldásával.

a) A terv szerint összesen mennyi időt szán Vera az utolsó 4 feladat megoldására?

A versenyzőknek minden feladat megoldása után öt lehetséges válasz közül kell az egyetlen helyes választ kiválasztaniuk. Egy versenyző pontszámának kiszámítása a 4·H – R + F képlettel történik, ahol H a helyes válaszok, R a rossz válaszok, F pedig a kitűzött feladatok számát jelenti (a kihagyott feladatokra 0 pont jár). Vera a 25 kitűzött feladat közül 3-at hagyott ki, és összesen 93 pontot szerzett.

b) Hány helyes választ adott Vera?

Vera osztályából összesen 11-en indultak a versenyen. Közülük ugyanannyian oldották meg a 24-es, mint a 25-ös feladatot. Sőt, ugyanennyien voltak azok is, akik a két feladat egyikét sem oldották meg. Egy olyan versenyző volt az osztályban, aki a 24-es és a 25-ös feladatot is megoldotta.

c)Hányan voltak az osztályban azok, akik a 24-es feladatot megoldották, de a 25-ös feladatot nem?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba