Adott az $ f $ és a $ g $ függvény.

$f:D_f=\mathbb{R}\setminus\left\{ k\cdot \dfrac{\pi} 2;\ k\in\mathbb{Z}\right\}\qquad \to (tg x+ctg x)\cdot \sin x $

a) Igazolja, hogy az így definiált $ f $ függvény konstans!

$ g:D_g=[-7;7]\qquad x\to x^2-6|x|$

b) Számítsa ki a $ g $ függvény zérushelyeit!

c) Adja meg a $ g $ függvény értékkészletét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Kilenc számkártya fekszik az asztalon.

a) Rakja négy csoportba a kilenc számkártyát úgy, hogy egyikben se legyen együtt egy szám és egy nála kisebb osztója! Adjon meg két lehetséges csoportosítást!

b) Berci körbe rakta a kilenc számkártyát egy nagy papírra, és ha két szám között legalább kettő volt a különbség, akkor a két kártyát összekötötte egy vonallal. Összesen hány vonalat rajzolt meg ily módon Berci?

Csaba az első hat kártya felhasználásával (1, 2, 3, 4, 5, 6) két háromjegyű számot készített. Hívjunk egy ilyen számpárt duónak. (Például egy lehetséges duó: "415 ; 362".) A hat számból több ilyen duót lehet készíteni. Két duót egyenlőnek tekintünk, ha ugyanaz a két különböző háromjegyű szám alkotja. Például a "415 ; 362" és a "362 ; 415" duó egyenlők, de a "362 ; 145" már egy másik duó.

c) Hány különböző duót lehet a hat számkártyából elkészíteni?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy mértani sorozat első három tagjának összege 91. A hatodik, a hetedik és a nyolcadik tag összege 2912. Hány tizenhárom-jegyű tagja van a sorozatnak?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy könyvkiadó minden negyedévben összesíti, hogy három üzletében melyik szépirodalmi kiadványából fogyott a legtöbb. A legutóbbi összesítéskor mindhárom üzletben ugyanaz a három szerző volt a legnépszerűbb: Arany János, Márai Sándor és József Attila. Az alábbi kördiagramok szemléltetik, hogy az üzletekben milyen arányban adták el ezeknek a szerzőknek a műveit. A kördiagramok az első üzletből 408, a másodikból 432, a harmadikból 216 eladott könyv eloszlásait szemléltetik.

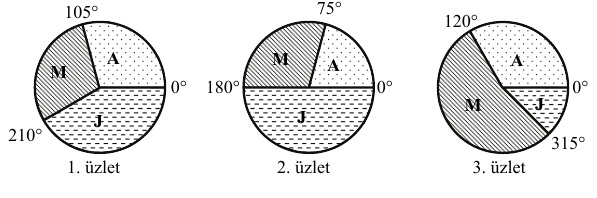
a) A kördiagramok adatai alapján töltse ki az alábbi táblázatot! Melyik szerző műveiből adták el a vizsgált időszakban a legtöbb könyvet?

b) Készítsen olyan oszlopdiagramot a táblázat alapján, amely a vizsgált időszakban a szerzők szerinti összesített forgalmat szemlélteti!

A könyvkiadó a három üzletében minden eladott könyvhöz ad egy sorsjegyet. Ezek a sorsjegyek egy közös sorsoláson vesznek részt negyedévenként. A vizsgált időszakban azok a sorsjegyek vesznek részt a sorsoláson, amelyeket a fenti három szerző műveinek vásárlói kaptak. Két darab 50 ezer forintos könyvutalványt sorsolnak ki köztük.

c) Mennyi annak a valószínűsége, hogy a vizsgált időszak sorsolásán mind a két nyertes sorsjegyet Márai Sándor egy-egy könyvéhez adták, és mindkét könyvet a 2. üzletben vásárolták? Válaszát három tizedesjegy pontossággal adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy áruházban egy mosóport négyféle kiszerelésben árusítanak. Az első kiszerelés $ 50\% $-kal drágább a harmadiknál, és $ 20\% $-kal kevesebb mosópor van benne, mint a másodikban. A második $ 50\% $-kal több mosóport tartalmaz, mint a harmadik, és $ 25\% $-kal többe kerül, mint az első.

a) Az első három kiszerelés közül melyikben a legalacsonyabb a mosópor egységára?

A negyedik fajta kiszerelést úgy állították össze, hogy annak dobozán a feltüntetett egységár megegyezett az első három kiszerelés átlagos egységárával.

b) Ha a legolcsóbb kiszerelésű dobozon 600 Ft egységárat tüntettek fel, akkor hány forint egységár szerepel a negyedik fajta dobozon?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen $ f(x)=-\dfrac{4x^3} a+\dfrac{3x^2} a+\dfrac{2x} a-a$, ahol $ a $ pozitív valós szám és $ x \in \mathbb{R} $.

a) Igazolja, hogy $ \int\limits_{0}^{a} f(x)\ dx= = - a^3 + a $.

b) Mely pozitív valós $ a $ számokra teljesül, hogy $ \int\limits_{0}^{a} f(x)\ dx\ge0$

c) Az $ x $ mely pozitív valós értéke esetén lesz a $ g(x) = -x^3 + x $ függvénynek lokális (helyi) maximuma?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ ABCD $ konvex négyszög oldalegyeneseinek egyenlete rendre:

$ DA: 3x - 4y - 20 = 0 $ , $ AB: 3x + 5y - 20 = 0 $ , $ BC: 4x - 3y +12 = 0 $, $ CD: 5x + 3y +15 = 0 $ .

a) Igazolja, hogy a négyszög átlói az $ x $ és az $ y $ tengelyre illeszkednek, továbbá hogy ennek a négyszögnek nincsen derékszöge!

b) Bizonyítsa be, hogy ez a négyszög húrnégyszög!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Peti levelet írt négy barátjának, Andrásnak, Bélának, Csabának és Daninak, és mindenkinek 1-1 fényképet is akart küldeni a nyaralásról. A négy fénykép különböző volt, és Peti mindegyikük hátlapjára ráírta, kinek szánja. A fényképeket végül figyelmetlenül rakta borítékba, bár mindenki kapott a levelében egy fényképet is.

a1) Hányféleképpen fordulhat elő, hogy csak Andris kapja azt a fényképet, amelyen a saját neve szerepel?

a2) Melyik esemény bekövetkezésének nagyobb a valószínűsége:

- senki sem kapja azt a fényképet, amelyet Peti neki szánt;

vagy

- pontosan egyikük kap olyan fényképet, amelyen a saját neve szerepel?

b) Egy szabályos érme egyik oldalán a 6-os, a másikon pedig a 4-es számjegy látható. Az érmét négyszer egymás után feldobjuk, és a dobott számokat összeadjuk. Milyen értékeket kaphatunk összeg gyanánt? Az egyes összegek dobásának mekkora a valószínűsége?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy $ 90\ m^2 $ területű, trapéz alakú virágágyás párhuzamos oldalainak aránya $ AB : DC = 3: 2 $ . Az ágyást tavasszal és ősszel is az évszaknak megfelelő virágokkal ültetik be. Mindkét alkalommal mindegyik fajta virágból átlagosan 50 virágtövet ültetnek négyzetméterenként. Tavasszal az átlókkal kijelölt négy háromszögre bontották a virágágyást. Az $ ABM $ háromszögbe sárga virágokat, a $ DMC $ háromszögbe fehéret, a maradék két részbe piros virágokat ültettek.

a) A tavaszi parkosításkor hány darab fehér, hány piros és hány sárga virágot ültettek be?

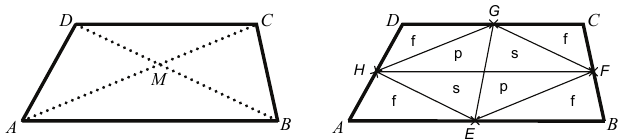
Ősszel a másik ábra alapján tervezték meg a virágok elhelyezését. (Az E, F, G és H pontok a trapéz oldalainak felezőpontjai.) Ekkor is fehér (f), piros (p) és sárga (s) virágokat ültettek a tervrajz alapján.

b) Az őszi parkosításkor hány darab fehér, hány piros és hány sárga virágot ültettek? Válaszait az alábbi táblázatban tüntesse fel!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Mely valós számok elégítik ki az alábbi egyenlőtlenséget?

$(x-1)^3-(x+1)^3>-8 $

b) Az alábbi $ f $ és $ g $ függvényt is a $ [- 3 ; 6] $ intervallumon értelmezzük. $ f (x) = \sqrt{ x + 3 } $ és $ g(x) = -0,5x + 2,5 $. Ábrázolja közös koordinátarendszerben az $ f $ és a $ g $ függvényt a $ [- 3 ; 6] $ intervallumon! Igazolja számolással, hogy a két grafikon metszéspontjának mindkét koordinátája egész szám!

c) Oldja meg az alábbi egyenlőtlenséget a valós számok halmazán!

$ 0,5x + \sqrt{ x + 3 } \le 2,5 $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Hány olyan tízjegyű pozitív egész szám van, amelynek minden számjegye a $ \{0 ; 8\} $ halmaz eleme?

b) Írja fel a 45-nek azt a legkisebb pozitív többszörösét, amely csak a 0 és a 8-as számjegyeket tartalmazza!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ ABCDEFGH $ téglatest A csúcsból induló élei: $ AB=12 $; $ AD=6 $; $ AE=8 $. Jelölje a $ HG $ él felezőpontját $ P $.

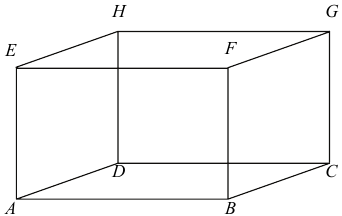
a) Számítsa ki az $ ABCDP $ gúla felszínét!

b) Mekkora szöget zár be az $ ABCDP $ gúla $ ABP $ lapjának síkja az $ ABCD $ lap síkjával?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy felmérés során megkérdeztek 640 családot a családban élő gyermekek számáról, illetve azok neméről. A felmérés eredményét az alábbi táblázat mutatja:

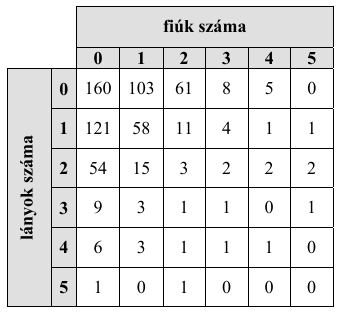
(Tehát pl. a gyermektelen családoknak a száma 160, és 15 olyan család volt a megkér- dezettek között, amelyben 1 fiú és 2 lány van.)

a) Hány fiúgyermek van összesen a megkérdezett családokban?

b) A felmérésben szereplő legalább kétgyermekes családokban mennyi a leggyakoribb leányszám?

c) A családsegítő szolgálat a megkérdezett családok közül a legalább négy gyermeket nevelőket külön támogatja. Az alábbi táblázat kitöltésével készítsen gyakorisági táblázatot a külön támogatásban részesülő családokban lévő gyermekek számáról!

Hány családot és összesen hány gyermeket támogat a családsegítő szolgálat?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A $ x^2 = 2 y $ egyenletű parabola az $ x^2 + y^2\le 8 $egyenletű körlapot két részre vágja. Mekkora a konvex rész területe? Számolása során ne használja a $ \pi $ közelítő értékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Megrajzoltuk az ABCDE szabályos ötszöget, és berajzoltuk minden átlóját. Az átlók metszéspontjait az ábra szerint betűztük meg: P, Q, R, S, T.

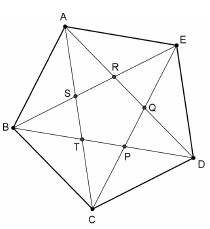
a) Hány olyan háromszög látható az ábrán, amelynek mindhárom csúcsa a megjelölt 10 pont közül való, és mindhárom oldalegyenese az ABCDE ötszög oldalegyenesei és átlóegyenesei közül kerül ki? Hány lényegesen különböző háromszög van ezek között, ha az egymáshoz hasonló háromszögeket nem tekintjük lényegesen különbözőknek?

b) Tudjuk, hogy az ABCQ négyszög területe 120 cm2 . Mekkora az ABCDE ötszög területe? Válaszát egész értékre kerekítve adja meg!

c) Tekintsük azt a tíz csúcsú gráfot, amelyet a megadott ábra szemléltet. Erről a gráfról fogalmaztunk meg két állítást. Állapítsa meg mindkét állításról, hogy igaz vagy hamis! Adjon rövid magyarázatot válaszára!

1. állítás: Ennek a gráfnak 20 éle van.

2. állítás: Ebben a gráfban van olyan részgráf, amely nyolc élű kör.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy kozmetikumokat gyártó vállalkozás nagy tételben gyárt egyfajta krémet. A termelés teljes havi mennyisége (x kilogramm) 100 és 700 kg közé esik, amelyet egy megállapodás alapján a gyártás hónapjában el is adnak egy nagykereskedőnek. A megállapodás azt is tartalmazza, hogy egy kilogramm krém eladási ára: $ (36-0,03x) $ euró. A krémgyártással összefüggő havi kiadás (költség) is függ a havonta eladott mennyiségtől. A krémgyártással összefüggő összes havi kiadást (költséget) a $ 0 , 0001 x ^{3} - 30 , 12 x + 13 000 $ összefüggés adja meg, szintén euróban.

a) Számítsa ki, hogy hány kilogramm krém eladása esetén lesz az eladásból származó havi bevétel a legnagyobb! Mekkora a legnagyobb havi bevétel?

b) Adja meg a krémgyártással elérhető legnagyobb havi nyereséget! Hány kilogramm krém értékesítése esetén valósul ez meg? (nyereség=bevétel–kiadás)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Két gyerek mindegyike 240 forintért vett kaparós sorsjegyet. Fémpénzzel fizettek (5; 10, 20, 50, 100 és 200 forintos érmékkel), és pontoson kiszámolták a fizetendő összeget. Hányféleképpen fizethetett Miki, ha ő 4 darab érmével fizetett, és hányféleképpen fizethet Karcsi, ha ő 5 darab érmével fizetett? (A pénzérmék átadási sorrendjét nem vesszük figyelembe.) A "bergengóc" lottóban kétszer húznak egy játéknapon. Bandi egy szelvénnyel játszik, tehát az adott játéknapon mindkét húzásnál nyerhet ugyanazzal a szelvénnyel.

b) Mekkora annak a valószínűsége, hogy egy adott játéknapon Bandinak legalább egy telitalálata lesz, ha $ p $ annak a valószínűsége $ ( 0 < p < 1 ) $, hogy egy szelvényen, egy húzás esetén telitalálata lesz? Megváltoztatták a játékszabályokat: minden játéknapon csak egyszer húznak (más játékszabály nem változott). Bandi most két (nem feltétlenül különbözően kitöltött) szelvénnyel játszik.

c) Mekkora annak a valószínűsége, hogy egy adott játéknapon Bandinak telitalálata legyen valamelyik szelvényén?

d) A telitalálat szempontjából a b) vagy a c)-ben leírt játék kedvezőbb Bandi számára?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy egyetem 10 580 hallgatójának tanulmányi lapjáról összesítették az angol és német nyelvvizsgák számát. Kiderült, hogy a német nyelvvizsgával nem rendelkezők $ 70\% $-ának, a német nyelvvizsgával rendelkezők $ 30\% $-ának nincs angol nyelvvizsgája. Az angol nyelvvizsgával nem rendelkezők $ 60\% $-ának német nyelvvizsgája sincs.

a) Ezek közül a hallgatók közül hányan rendelkeztek angol és hányan német nyelvvizsgával?

b) A hallgatók hány százaléka rendelkezett az angol és német nyelvvizsgák mindegyikével?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen $ A = \{ x \in\mathbb{R} \sqrt{ x - 1 } \ge \sqrt{ 5 - x } \} $ és $ B = \left\{ x \in\mathbb{R} | \log_{\dfrac{ 1}{2 }} ( 2 x - 4 ) > -2 \right\} $. Adja meg az $ \left\{ A\cup B \right\} $, $\left\{ A\cap B \right\}$ , $\left\{ B \setminus A \right\}$ halmazokat!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy város sportklubjának 640 fős tagságát felnőttek és diákok alkotják. A tagság $ 55\% $-a sportol rendszeresen. A rendszeresen sportoló tagok számának és a sportklub teljes taglétszámnak az aránya 11 -szor akkora, mint a rendszeresen sportoló felnőttek 8 számának aránya a felnőtt klubtagok számához viszonyítva. A rendszeresen sportolók aránya a felnőtt tagságban fele akkora, mint amekkora ez az arány a diákok között. Hány felnőtt és hány diák tagja van ennek a sportklubnak?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy gyártósoron 8 darab gép dolgozik. A gépek mindegyike, egymástól függetlenül 0,05 valószínűséggel túlmelegszik a reggeli bekapcsoláskor. Ha a munkanap kezdetén 3 vagy több gép túlmelegszik, akkor az egész gyártósor leáll. A 8 gép reggeli beindításakor bekövetkező túlmelegedések számát a binomiális elosz- lással modellezzük.

a) Adja meg az eloszlás két paraméterét! Számítsa ki az eloszlás várható értékét!

b) Mennyi annak a valószínűsége, hogy a reggeli munkakezdéskor egyik gép sem melegszik túl?

c) Igazolja a modell alapján, hogy (négy tizedes jegyre kerekítve) 0,0058 annak a valószínűsége, hogy a gépek túlmelegedése miatt a gyártósoron leáll a termelés a munkanap kezdetekor!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ A_1C_0C_1 $ derékszögű háromszögben az $ A_1 $ csúcsnál $ 30^\circ $-os szög van, az $ A_1C_0 $ befogó hossza 1, az $ A_1C_1 $ átfogó felezőpontja $ A_2 $. Az $ A_2C_1 $ szakasz "fölé" az $ A_1C_0 C_1 $ háromszöghöz hasonló $ A_2 C_1C_2 $ derékszögű háromszöget rajzoljuk az ábra szerint.

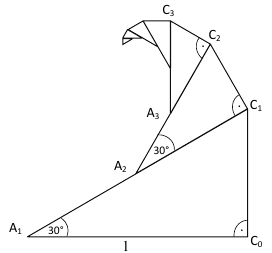
Az $ A_2C_2 $ átfogó felezőpontja $ A_3 $. Az $ A_3C_2 $ szakasz "fölé" az $ A_2C_1 C_2 $ háromszöghöz hasonló $ A_3 C_2C_3 $ derékszögű háromszöget rajzoljuk. Ez az eljárás tovább folytatható.

a) Számítsa ki az így nyerhető végtelen sok derékszögű háromszög területének összegét (az összeg első tagja az $ A_1C_0C_1 $ háromszög területe)!

b) Igazolja, hogy a $ C_0C_1C_2...C_n $ töröttvonal hossza minden pozitív egész n-re kisebb, mint $ 1,4 $.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adott a síkbeli derékszögű koordináta-rendszerben az $ x^{ 2} + y^ 2 + 6 x + 4 y - 3 = 0 $ egyenletű kör. Ebbe a körbe szabályos háromszöget írunk, amelynek egyik csúcsa $ A(1; –2) $.

a) Számítsa ki a szabályos háromszög másik két csúcsának koordinátáit! Pontos értékekkel számoljon!

b) Véletlenszerűen kiválasztjuk az adott kör egy belső pontját. Mekkora a valószínűsége annak, hogy a kiválasztott pont a tekintett szabályos háromszögnek is belső pontja? Válaszát két tizedes jegyre kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A nyomda egy plakátot 14 400 példányban állít elő. A költségeket csak a nyomtatáshoz felhasznált nyomólemezek (klisék) darabszámának változtatásával tudják befolyásolni. Egy nyomólemez 2500 Ft-ba kerül, és a nyomólemezek mindegyikével óránként 100 plakát készül el. A nyomólemezek árán felül, a lemezek számától függetlenül, minden nyomtatásra fordított munkaóra további 40 000 Ft költséget jelent a nyomdának. A ráfordított idő és az erre az időre jutó költség egyenesen arányos.

a) Mennyi a nyomólemezek árának és a nyomtatásra fordított munkaórák miatt fellépő költségnek az összege, ha a 14 400 plakát kinyomtatásához 16 nyomólemezt használnak?

b) A 14 400 plakát kinyomtatását a nyomda a legkisebb költséggel akarja megoldani. Hány nyomólemezt kell ekkor használnia? Mennyi ebben az esetben a nyomólemezekre és a ráfordított munkaidőre jutó költségek összege?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy fából készült négyzetes oszlop minden élének hossza centiméterben mérve 2-nél nagyobb egész szám. A négyzetes oszlop minden lapját befestettük pirosra, majd a lapokkal párhuzamosan 1 cm élű kis kockára vágtuk. A kis kockák közül 28 lett olyan, amelynek pontosan két lapja piros. Mekkora lehetett a négyzetes oszlop térfogata?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Hány $ (x; y) $ rendezett valós számpár megoldása van az alábbi egyenletrendszernek, ha $ x $ és $ y $ is a$ [ 0 ; 2\pi ] $ zárt intervallum elemei?

$\begin{cases} \sin x \cdot \cos y = 0 \\ \sin x + \sin^2 y = \dfrac 1 4  \end{cases} $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Kinga 10. születésnapja óta kap havi zsebpénzt a szüleitől. Az első összeget a 10. születésnapján adták a szülők, és minden hónapban 50 Ft-tal többet adnak, mint az azt megelőző hónapban. Egy bizonyos hónapban, mikor éppen 1850 Ft volt a havi zsebpénze, összeadta az addig kapott összes zsebpénzét. Az összeg 35100 Ft lett. Mennyi volt Kinga induló zsebpénze, és hány hónap telt el a 10. születésnapja óta?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ENSZ 1996-ban megjelent táblázatának egy részlete a nyolc legnagyobb népességszámú ország népességi adatait tartalmazza 1988-ban, és egy népesedésdinamikai modell előrejelzése alapján 2050-ben.

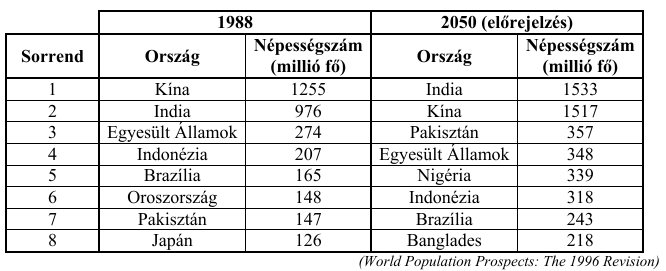
Feltételezzük, hogy Pakisztán lakossága 1988 és 2050 között minden évben ugyanannyi százalékkal nő, mint amennyi százalékkal az előző évben növekedett.

a) Ezzel a feltételezéssel élve - millió főre kerekítve - hány lakosa lesz Pakisztánnak 2020-ban? (Az évi százalékos növekedés két tizedesjegyre kerekített értékével számoljon!)

b) A táblázat mindkét oszlopában szereplő országok népességi adataira vonatkozóan mennyivel változik az átlagos lakosságszám és a medián 1988 és 2050 között? (Válaszát millió főben, két tizedesjegyre kerekítve adja meg.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 32 fős érettségiző osztály tanulói három különböző táncot mutatnak be a szalagavató bálon. Az alábbi táblázat az egyes táncokban fellépő diákok számát mutatja nemenkénti bontásban.

Van 2 olyan lány, aki mindhárom táncban fellép, ugyanakkor nincs olyan fiú az osztályban, aki egynél több produkcióban részt venne.

a) A lányok közül kettőt véletlenszerűen kiválasztva, mennyi annak a valószínűsége, hogy mindketten táncolnak a kán-kánban?

b) Az osztály tanulói közül egyet véletlenszerűen kiválasztva, mennyi a valószínűsége annak, hogy az illető pontosan két táncban szerepel?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba